ANGLES: COMPLEMENTARY, SUPPLEMENTARY,
VERTICAL, and LINEAR PAIRS
For this web exercise, assume all angles are measured in degrees.
In particular:
- if $\,\angle 1\,$ and $\,\angle 2\,$ are complementary, then $\,m\angle 1+ m\angle 2 = 90^{\circ}\,$
- if $\,\angle 1\,$ and $\,\angle 2\,$ are supplementary, then $\,m\angle 1+ m\angle 2 = 180^{\circ}\,$
DEFINITION
opposite rays
Rays that:
|
|
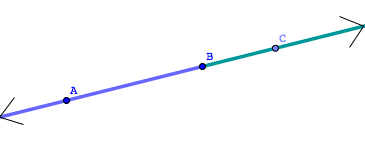
Note:
If three points are on a line
with $\,B\,$ between $\,A\,$ and $\,C\,$,
then
$\,\overrightarrow{BA}\,$
and
$\,\overrightarrow{BC}\,$
are opposite rays.
Recall that both $\,A{-}B{-}C\,$ and $\,C{-}B{-}A\,$
are notation for ‘$\,B\,$ is between $\,A\,$ and $\,C\,$’.
DEFINITION
linear pair
Two angles are a linear pair
iff
|
|
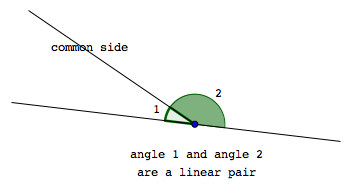
Note: If $\,\angle 1\,$ and $\,\angle 2\,$ are a linear pair, then $\,m\angle 1+ m\angle 2 = 180^{\circ}\,$.
DEFINITION
vertical angles
| Two angles are vertical angles iff the sides of one angle are opposite rays to the sides of the other. |
|
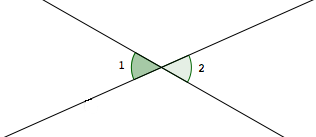
Note: Vertical angles are the ‘opposite angles’ that are formed by two intersecting lines.
Note: If $\,\angle 1\,$ and $\,\angle 2\,$ are vertical angles, then $\,m\angle 1 = m\angle 2\ $.
DEFINITION
parallel lines
Two lines are parallel
if and only if
they lie in the same plane and do not intersect.
Parallel lines are studied in more detail in a future section, Parallel Lines.
The symbol ‘$\,\parallel\,$’ is used to denote parallel lines.
The sentence
‘$\,\ell\parallel m\,$’
is read as
‘$\,\ell \,$ is parallel to $\,m\,$’,
and is true precisely when line
$\,\ell\,$ is parallel to
line $\,m\,$.
DEFINITION
perpendicular lines
Two lines are perpendicular
if and only if
they form a right angle.
The symbol ‘$\,\perp\,$’ is used to denote perpendicular lines.
The sentence
‘$\,\ell\perp m\,$’
is read as
‘$\,\ell \,$ is perpendicular to $\,m\,$’,
and is true precisely when line
$\,\ell\,$ is perpendicular to
line $\,m\,$.
EXAMPLE:
Question:
Suppose that $\,\angle 1\,$ and
$\,\angle 2\,$ are vertical angles.
Suppose that $\,m\angle 1 = 7x-15\,$ and $\,m\angle 2 = 2x+55\,$.
Find $\,x\,$.
Suppose that $\,m\angle 1 = 7x-15\,$ and $\,m\angle 2 = 2x+55\,$.
Find $\,x\,$.
Solution:
| $7x-15= 2x+55$ | (vertical angles have equal measures) |
| $5x-15=55$ | (subtract $\,2x\,$ from both sides) |
| $5x=70$ | (add $\,15\,$ to both sides) |
| $x=14$ | (divide both sides by $\,5\,$) |
Master the ideas from this section
by practicing the exercise at the bottom of this page.
When you're done practicing, move on to:
Equivalence Relations
by practicing the exercise at the bottom of this page.
When you're done practicing, move on to:
Equivalence Relations