 Solving Simple Absolute Value Sentences
Solving Simple Absolute Value Sentences
Need some simpler practice with absolute value first?
- Simplifying Basic Absolute Value Expressions
- Determining the Sign (positive or negative) of Absolute Value Expressions
Recall that $\,|x|\,$ gives the distance between $\,x\,$ and $\,0\,.$ If you think in terms of distance, then it's easy to solve sentences involving absolute value!
Example: An Absolute Value Equation
Note: We want all numbers $\,x\,$ whose distance from zero is $\,3\,.$
$$ \cssId{s16}{\overset{\text{whose distance from zero ...}}{\overbrace{\ |\overset{\text{want numbers $\,x\,$... }}{\ \strut x\ }|\ }} \overset{\text{is ...}}{\strut \ \ \ =\ \ \ } \overset{\text{three}}{\strut 3}} $$The diagram above shows how the sentence is telling you what you want! Interpret it in the following order:
| 1) | We want numbers $\,x\,$... | the unknown is $\,x\,$ |
| 2) | whose distance from zero ... | the vertical bars, $|\ |\,,$ ask for distance from zero |
| 3) | is ... | the equal sign |
| 4) | $3$ | three |
Remember that you can ‘walk’ from zero in two directions: to the right, and to the left. The number $\,3\,$ is three units from zero to the right; the number $\,-3\,$ is three units from zero to the left.

The word ‘or’ in the sentence ‘$\,x=3\text{ or }x=-3\,$’ is the mathematical word ‘or’. You may want to review its meaning: Practice with the Mathematical Words ‘and’, ‘or’, ‘is equivalent to’
Example: An Absolute Value Inequality Involving ‘Less Than’
Note: We want all numbers $\,x\,$ whose distance from zero is less than $\,3\,.$
$$ \cssId{s40}{\overset{\text{whose distance from zero ...}}{\overbrace{\ |\overset{\text{want numbers $\,x\,$... }}{\ \strut x\ }|\ }} \overset{\text{is less than ...}}{\strut \ \ \ \ \ \lt\ \ \ \ \ } \overset{\text{three}}{\ \ \ \ \strut 3\ \ \ \ }} $$The diagram above shows how the sentence is telling you what you want! Interpret it in the following order:
| 1) | We want numbers $\,x\,$... | the unknown is $\,x\,$ |
| 2) | whose distance from zero ... | the vertical bars, $|\ |$, ask for distance from zero |
| 3) | is less than ... | the ‘less than’ symbol |
| 4) | $3$ | three |
You can walk less than three units to the right—this gets you the numbers from $\,0\,$ to $\,3\,.$ You can walk less than three units to the left—this gets you the numbers from $\,0\,$ to $\,-3\,.$ Together, you end up with all the numbers between $\,-3\,$ and $\,3\,$:
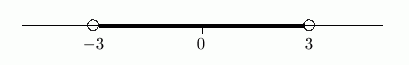
The sentence ‘$\,-3 \lt x \lt 3\,$’ is just a shorthand for ‘$\,-3\lt x\,$ and $\,\ x \lt 3\,$’. That's the mathematical word ‘and’. You may want to review its meaning: Practice with the Mathematical Words ‘and’, ‘or’, ‘is equivalent to’
The shorthand ‘$\,-3\lt x\lt 3\,$’ is a great shorthand, because you see an $\,x\,$ trapped between $\,-3\,$ and $\,3\,$; and those are precisely the values of $\,x\,$ that make the sentence true.
Example: An Absolute Value Inequality Involving ‘Greater Than’
Note: We want all numbers $\,x\,$ whose distance from zero is greater than $\,3\,.$
$$ \cssId{s66}{\overset{\text{whose distance from zero ...}}{\overbrace{\ |\overset{\text{want numbers $\,x\,$... }}{\ \strut x\ }|\ }} \overset{\text{is greater than ...}}{\strut \ \ \ \ \ \gt\ \ \ \ \ } \overset{\text{three}}{\ \ \ \ \strut 3\ \ \ \ }} $$The diagram above shows how the sentence is telling you what you want! Interpret it in the following order:
| 1) | We want numbers $\,x\,$... | the unknown is $\,x\,$ |
| 2) | whose distance from zero ... | the vertical bars, $|\ |$, ask for distance from zero |
| 3) | is greater than ... | the ‘greater than’ symbol |
| 4) | $3$ | three |
You can walk more than three units to the right—this gets you all the numbers to the right of $\,3\,.$ You can walk more than three units to the left—this gets you all the numbers to the left of $\,-3\,.$ Together, you end up with the two pieces shown below:

The word ‘or’ in the sentence ‘$\,x\lt -3\,$ or $\, x\gt 3\,$’ is the mathematical word ‘or’. You may want to review its meaning: Practice with the Mathematical Words ‘and’, ‘or’, ‘is equivalent to’
Example: An Absolute Value Sentence With No Solutions
Example: An Absolute Value Sentence That Is Always True
Concept Practice
Solve the given absolute value sentence. Write the result in the most conventional way.
For more advanced students, a graph is available. For example, the equation $\,|x| = 3\,$ is optionally accompanied by the graph of $\,y = |x|\,$ (the left side of the equation, dashed green) and the graph of $\,y = 3\,$ (the right side of the equation, solid purple). In this example, you are finding the values of $\,x\,$ where the green graph intersects the purple graph.
Click the ‘Show/Hide Graph’ button to toggle the graph.