 Finding the Greatest Common Factor of 2 or 3 Numbers
Finding the Greatest Common Factor of 2 or 3 Numbers
Example
The idea:
| The factors of $\,27\,$ are: | $\,1\,$ | $\,3\,$ | $\,9\,$ | $\,27$ | |||
| The factors of $\,18\,$ are: | $\,1\,$ | $\,2\,$ | $\,3\,$ | $\,6\,$ | $\,9\,$ | $\,18\,$ |
The common factors of $\,27\,$ and $\,18\,$ (the numbers that appear in both lists) are $\,1\,,$ $\,3\,,$ and $\,9\,.$
The greatest common factor (the greatest number in the list of common factors) is $\,9\,.$
Efficient Algorithm for Finding the Greatest Common Factor
Here's an efficient algorithm for finding the greatest common factor, when there aren't too many numbers, and they aren't too big.
The process is illustrated by finding the greatest common factor of $\,18\,,$ $\,36\,,$ and $\,90\,$:
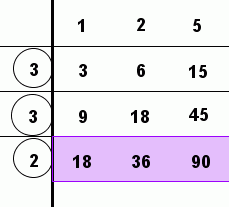
- Line up the numbers in a row. (See the purple rectangle.)
- Find any number that goes into everything evenly (like $\,2\,$).
-
Do the divisions,
and write the results above the original numbers.
In the example:
- $18\,$ divided by $\,2\,$ is $\,9\,$; write the $\,9\,$ above the $\,18\,$
- $36\,$ divided by $\,2\,$ is $\,18\,$; write the $\,18\,$ above the $\,36\,,$ and so on
- Keep repeating the process, until there isn't any number (except $\,1\,$) that goes into everything evenly.
- Multiply the circled numbers together. This is the greatest common factor!
- In the example, $\,\text{gcf}(18,36,90) = 2\cdot 3\cdot 3 = 18\,.$
Why Does This Method Work?
Think about why this method works. As you walk through each step of this discussion, keep comparing with the chart above.
Look at the prime factorizations of each number:
The number $\,2\,$ goes into each evenly, so separate it off:
The number $\,3\,$ goes into each remaining part evenly, so separate it off:
Here's the final step:
Other Ways to Apply the Algorithm
Here are some other ways the algorithm might be applied. Of course, you get the same answer any correct way that you do it!
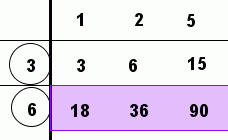
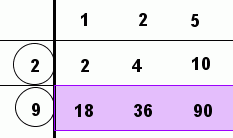
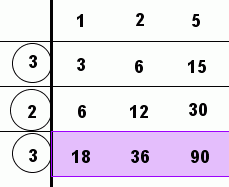
You can also zip over to wolframalpha.com and type in gcd(18,36,90). The ‘gcd’ stands for greatest common divisor, which is another name for greatest common factor.