Working with Linear Functions: Finding a New Point,
Given a Point and a Slope
Suggested review of lines from the Algebra I curriculum:
Recall:
$$ \begin{align} &\cssId{s7}{\text{slope of line through points } (x_1,y_1) \text{ and } (x_2,y_2)}\cr\cr &\qquad \cssId{s8}{=\ \ m}\cr\cr &\qquad \cssId{s9}{=\ \ \frac{\text{rise}}{\text{run}}}\cr\cr &\qquad\cssId{s10}{=\ \ \frac{\text{change in } y}{\text{change in } x}}\cr\cr &\qquad\cssId{s11}{=\ \ \frac{\Delta y}{\Delta x}}\cr\cr &\qquad\cssId{s12}{=\ \ \frac{y_2 - y_1}{x_2 - x_1}} \end{align} $$A common scenario is (see diagram below):
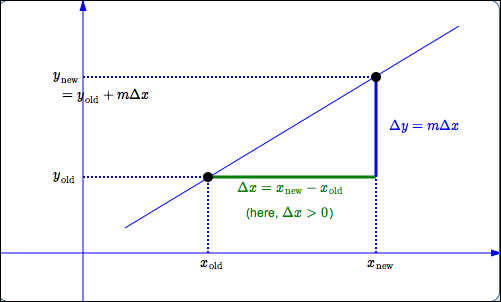
- You have a line with known slope $\,m\,.$
- You know the coordinates of one point on the line. Call this known point $(x_{\text{old}},y_{\text{old}})\,.$
- There is another point on the line whose coordinates are needed. Call this desired point $(x_{\text{new}},y_{\text{new}})\,.$
-
You know the change in $\,x\,$
between the old and new point:
$$
\cssId{s20}{\Delta x = x_{\text{new}} - x_{\text{old}}}
$$
$$ \begin{gather} \cssId{s21}{\Delta x \gt 0}\cr \cssId{s22}{\text{is equivalent to}}\cr \cssId{s23}{\text{the new point lies to the right of the old point}}\cr\cr\cr \cssId{s24}{\Delta x \lt 0}\cr \cssId{s25}{\text{is equivalent to}}\cr \cssId{s26}{\text{the new point lies to the left of the old point}} \end{gather} $$ - You want the $y$-coordinate, $\,y_{\text{new}}\,,$ of the new point.
- Solving for $\,y_{\text{new}}\,$ in terms of the known quantities: $$ \begin{align} &\cssId{s29}{m = \frac{y_{\text{new}} - y_{\text{old}}}{x_{\text{new}} - x_{\text{old}}}}\cr &\qquad \cssId{s30}{\Rightarrow}\ \ \cssId{s31}{y_{\text{new}} - y_{\text{old}} = m \overbrace{(x_{\text{new}} - x_{\text{old}})}^{\Delta x}}\cr\cr &\qquad \cssId{s32}{\Rightarrow}\ \ \cssId{s33}{y_{\text{new}} = y_{\text{old}} + \overbrace{m\Delta x}^{\Delta y}} \end{align} $$
Example
You have a known point $\,(1,-5)\,$ on a line with slope $\,7.5\,.$ When $\,x = 1.4\,,$ what is the $y$-value of the point on the line?
Solution: The change in $\,x\,$ in going from the known point ($\,x = 1\,$) to the new point ($\,x = 1.4\,$) is:
$$ \cssId{s39}{\Delta x = 1.4 - 1 = 0.4} $$ $$ \begin{align} \cssId{s40}{y_{\text{new}}}\ &\cssId{s41}{= y_{\text{old}} + m\Delta x}\cr &\cssId{s42}{= -5 + (7.5)(0.4)}\cr &\cssId{s43}{= -2} \end{align} $$