Trigonometric Values of Special Angles

With the work done in prior sections (particularly those listed below), we have everything needed to efficiently find exact values for things like $\,\cos\frac{81\pi}{4}\,$ and $\,\csc (-2640^\circ)\,.$

All the necessary tools/ideas are repeated below, in-a-nutshell. Having trouble following the brief discussion on this page? If so, review the links above (in order)—they offer a much slower and kinder approach.

Two Special Triangles

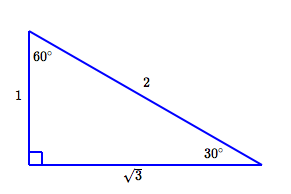
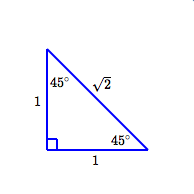
SOHCAHTOA

Sine Opposite Hypotenuse
Cosine Adjacent Hypotenuse
Tangent Opposite Adjacent

Reciprocal Relationships for Trig Functions

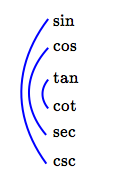
For example: $\displaystyle\csc = \frac{1}{\sin}$

Trigonometric Values of Small Special Angles

angle/number

sine, $\,\sin = \frac{\text{OPP}}{\text{HYP}}$

cosine, $\,\cos = \frac{\text{ADJ}}{\text{HYP}}$

tangent, $\,\tan = \frac{\text{OPP}}{\text{ADJ}}$

cotangent
(reciprocal of tangent)

secant
(reciprocal of cosine)

cosecant
(reciprocal of sine)

angle/number	$0^\circ = 0 \text{ rad}$
sine	$0$
cosine	$1$
tangent	$0$
cotangent	not defined
secant	$1$
cosecant	not defined

angle/number	$\displaystyle 30^\circ = \frac{\pi}{6} \text{ rad}$
sine	$\displaystyle\frac 12$
cosine	$\displaystyle\frac{\sqrt 3}2$
tangent	$\displaystyle\frac1{\sqrt 3} = \frac{\sqrt 3}{3} $
cotangent	$\sqrt 3$
secant	$\displaystyle\frac{2}{\sqrt 3} = \frac{2\sqrt 3}{3}$
cosecant	$2$

angle/number	$\displaystyle 45^\circ = \frac{\pi}{4} \text{ rad}$
sine	$\displaystyle\frac 1{\sqrt 2} = \frac{\sqrt 2}{2}$
cosine	$\displaystyle\frac 1{\sqrt 2} = \frac{\sqrt 2}{2}$
tangent	$1$
cotangent	$1$
secant	$\sqrt 2$
cosecant	$\sqrt 2$

angle/number	$ \displaystyle 60^\circ = \frac{\pi}{3} \text{ rad}$
sine	$\displaystyle\frac{\sqrt 3}{2}$
cosine	$\displaystyle \frac{1}{2}$
tangent	$\displaystyle \sqrt 3$
cotangent	$\displaystyle\frac1{\sqrt 3} = \frac{\sqrt 3}{3} $
secant	$2$
cosecant	$\displaystyle\frac{2}{\sqrt 3} = \frac{2\sqrt 3}{3}$

angle/number	$\displaystyle 90^\circ = \frac{\pi}{2} \text{ rad}$
sine	$1$
cosine	$0$
tangent	not defined
cotangent	$0$ ($\cot := \frac{\cos}{\sin}$)
secant	not defined
cosecant	$1$

Signs ($\pm$) of Sine, Cosine, and Tangent in All Quadrants

signs of sine, cosine, tangent in all quadrants

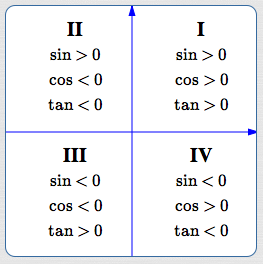
Reciprocals retain the sign ($+/-$) of the original number. Therefore, in all the quadrants:

Cosecant has the same sign as sine.
Secant has the same sign as cosine.
Cotangent has the same sign as tangent.

Trigonometric Values for Arbitrary Special Angles

In Special Triangles and Common Trigonometric Values, the ‘Locate-Shrink/Size-Signs’ method was introduced for finding trigonometric values of special angles. With additional tools and terminology now at hand, that discussion is presented more generally and efficiently here.

The RRQSS (Reduce-Reference/Quadrant-Size/Sign) Technique

Reduce:

[This step is optional. If your angle isn't too big (say, $\,510^\circ\,$ or $\,-\frac{7\pi}{3}\,$), then it may be easy for you to find its reference angle and quadrant, without ‘reducing’ it first. Your choice!]

As discussed in Reference Angles, remove any extra rotations from $\,\theta\,$:

$\theta\,$ in DEGREES

How many extra rotations (if any) in $\,\theta\,$?

To answer this question, compute $\,n := \frac{|\theta|}{360^\circ}\,,$ rounded to the nearest whole number.
If $\,\theta\,$ is positive, then replace $\,\theta\,$ by: $$\theta - n\cdot 360^\circ$$

If $\,\theta\,$ is negative, then replace $\,\theta\,$ by: $$\theta + n\cdot 360^\circ$$
Now, your angle/number is manageable: it is between $\,-180^\circ\,$ and $\,180^\circ\,.$ But, it has the same terminal point, so all the trigonometric values are the same!

$\theta\,$ in RADIANS

How many extra rotations (if any) in $\,\theta\,$?

To answer this question, compute $\,n := \frac{|\theta|}{2\pi}\,,$ rounded to the nearest whole number.
If $\,\theta\,$ is positive, then replace $\,\theta\,$ by: $$\theta - n\cdot 2\pi$$

If $\,\theta\,$ is negative, then replace $\,\theta\,$ by: $$\theta + n\cdot 2\pi$$
Now, your angle/number is manageable: it is between $\,-\pi\,$ and $\,\pi\,.$ But, it has the same terminal point, so all the trigonometric values are the same!

Reference/Quadrant:

Lay off $\,\theta\,$ in the standard way:

Start at the positive $x$-axis
Positive angles are swept out in a counterclockwise direction; start by going up
Negative angles are swept out in a clockwise direction; start by going down

Determine the reference angle/number for $\,\theta\,.$

Determine the quadrant for $\,\theta\,.$

Size/Sign:

Use the reference angle/number to find the correct size of the desired trigonometric value.

Use the quadrant to find the correct sign of the desired trigonometric value.

Examples

In this first example, the angles aren't too big, so the optional (reduce) step is skipped.

Find: $\,\sec 510^\circ\,$
Reduce	(skipped) [Dr. Burns would work with $\,510^\circ - 360^\circ = 150^\circ\,.$]
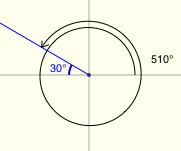
Reference/ Quadrant	$\,510^\circ\,$ is in quadrant II; the reference angle is $\,30^\circ\,$
Size/Sign	Size: $\displaystyle\sec 30^\circ = \frac{2}{\sqrt 3}\,$ Sign: In quadrant II, the secant is negative. Thus: $$\sec 510^\circ = -\frac{2}{\sqrt 3}$$

Find: $\displaystyle\,\cot (-\frac{7\pi}{3})\,$
Reduce	(skipped) [Dr. Burns would work with $\,-\frac{7\pi}3 + \frac{6\pi}3 = -\frac{\pi}3\,.$]
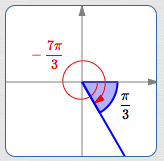
Reference/ Quadrant	$\displaystyle\,-\frac{7\pi}{3}\,$ is in quadrant IV; the reference angle is $\,\displaystyle\frac{\pi}{3}$
Size/Sign	Size: $\displaystyle\cot\frac{\pi}{3} = \frac{1}{\sqrt 3}\,$ Sign: In quadrant IV, the cotangent is negative. Thus: $$\cot(-\frac{7\pi}{3}) = -\frac{1}{\sqrt 3}$$

In this final example, the angles are very big, so get rid of extra rotations (reduce) in the first step:

Find: $\,\csc(-2640^\circ)$
Reduce	$$\cssId{s134}{\frac{\|\theta\|}{360^\circ} = \frac{2640^\circ}{360^\circ} \approx 7}$$ $$\cssId{s135}{-2640^\circ + 7\cdot 360^\circ = -120^\circ}$$ Work with $\,-120^\circ\,$ instead of $\,-2640^\circ\,.$
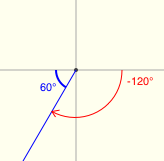
Reference/ Quadrant	$\,-120^\circ\,$ is in quadrant III; the reference angle is $\,60^\circ\,$
Size/Sign	SIZE: $\displaystyle\csc 60^\circ = \frac{2}{\sqrt 3}\,$ SIGN: In quadrant III, the cosecant is negative. Thus: $$\csc(-2640^\circ) = -\frac{2}{\sqrt 3}$$

Find: $\displaystyle\,\cos (\frac{81\pi}{4})\,$
Reduce	$$\cssId{s142}{\frac{\|\theta\|}{2\pi} = \frac{81\pi/4}{2\pi} \approx 10}$$ $$\cssId{s143}{\frac{81\pi}{4} - 10\cdot 2\pi = \frac{81\pi}{4} - \frac{80\pi}{4} = \frac{\pi}4}$$ Work with $\displaystyle\,\frac{\pi}4\,$ instead of $\displaystyle\,\frac{81\pi}4\,.$
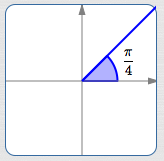
Reference/ Quadrant	$\,\frac{\pi}4\,$ is in quadrant I; the reference angle is $\,\displaystyle\frac{\pi}{4}$
Size/Sign	SIZE: $\displaystyle\cos\frac{\pi}{4} = \frac{1}{\sqrt 2}$ SIGN: In quadrant I, the cosine is positive. Thus: $$\cos\frac{81\pi}{4} = \frac{1}{\sqrt 2}$$