 Parametric Equations (Part 1)
Parametric Equations (Part 1)
(This page is Part 1. Click here for Part 2.)
An equation in two variables (like $\,y = x^2\,$) describes a set of points in the plane—the set of points $\,(x,y)\,$ that make the equation true.
However, it's a static collection of points, with no concept of the curve being ‘swept out’ (traced/drawn) in any particular way.
Parametric equations describe a curve that is swept out in a particular way!
To illustrate: The four graphs below have precisely the same set of points, but are swept out in different ways.
Measure time $\,t\,$ in (say) seconds. Then, each arrow below (connecting green points) represents a part of the curve traced out in one second.
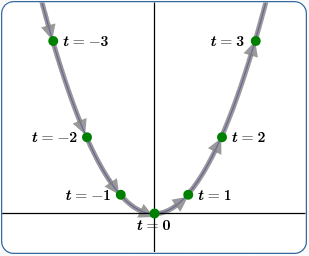
Example (1)
$x(t) = t\,$
$\,y(t) = t^2$
Swept out from left to right
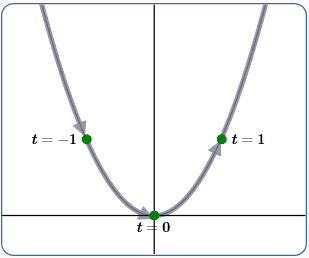
Example (2)
$x(t) = 2t\,$
$\,y(t) = (2t)^2 = 4t^2$
Swept from left to right, faster than in (1)
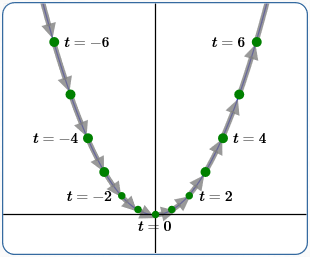
Example (3)
$x(t) = \frac 12t\,$
$\,y(t) = (\frac 12t)^2 = \frac{t^2}4$
Swept from left to right, slower than in (1)
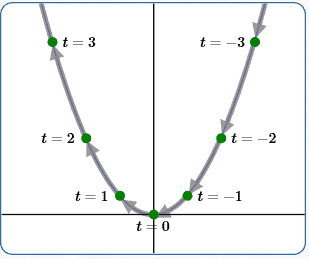
Example (4)
$x(t) = -t\,$
$\,y(t) = (-t)^2 = t^2$
Swept from right to left, same speed as in (1)
(Note: For better-sized images, the horizontal and vertical scales on each individual graph are different. However, all four graphs use precisely the same scales.)
What is a Parameter?
A parameter is a variable used in a special way: to identify particular members of a family of mathematical objects.
For example, consider the familiar equation $\,y = mx + b\,.$ Four variables appear in this equation ($\,x\,,$ $\,y\,,$ $\,m\,$ and $\,b\,$), but only two of them ($\,m\,$ and $\,b\,$) are parameters. Why?
The single equation ‘$\,y = mx + b\,$’ defines an entire family of equations. Choices for $\,m\,$ and $\,b\,$ determine which member of this ‘family’ you get! For example:
| Choosing these parameters ... | ... Gives this equation |
| $\,m = 2\,,$ $\,b = -1$ | $\,y = 2x - 1\,$ |
| $\,m = -3\,,$ $\,b = 0$ | $\,y = -3x\,$ |
| $\,m = 0\,,$ $\,b = 7\,$ | $\,y = 7\,$ |
| The list goes on and on! | |
As you'll learn below, parametric equations define a family of points instead of a family of equations, but the foundational idea is the same.
What are Parametric Equations?
Describe a curve in the following way:
- Choose a parameter. The variable $\,t\,$ is a common parameter choice, since it is often viewed as time.
-
Give formulas, as functions of $\,t\,,$ for both the $x$-values and $y$-values of points on the curve.
That is (using function notation) write:
$x(t) = \text{some function of $\,t\,$}$
(Read aloud as: ‘$\,x\,$ of $\,t\,$ is some function of $\,t\,$’)
$y(t) = \text{some function of $\,t\,$}$
(Read aloud as: ‘$\,y\,$ of $\,t\,$ is some function of $\,t\,$’)
Each of these equations is called a parametric equation. Together, these parametric equations describe a curve in a plane that is swept out in a particular way.
What is ‘Parametric’ about Parametric Equations?
When a curve is described by parametric equations, you naturally get a family of points:
All points of the form $\,\bigl(\,x(t)\,,\,y(t)\,\bigr)\,$ for the allowable values of $\,t$
The parameter $\,t\,$ is used to identify each particular point in this family!
Note:
- In the ‘$\,y = mx + b\,$’ example, $\,m\,$ and $\,b\,$ are parameters to identify members in a family of equations.
- Parametric equations use a parameter (denoted here by $\,t\,$) to identify members in a family of points.
Some Interesting Parametric Equations
Here are some parametric equations that are more interesting than the simple examples at the top of this page.
Arrows and gradually-changing color have been added, so you can see how the curve is traced out.
Curves (except for Einstein) begin at the green point, and end at the red point.
For a given image, each arrow represents a part of the curve traced out in a fixed amount of time—so longer arrows means that piece is traced out faster!
The first three examples have additional parameters (other than $\,t\,$), so each describes an entire family of curves.
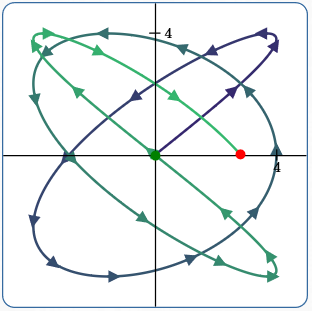
Example (5)
Play with Lissajous curves
$x(t) = A\sin(at + \delta)$
$y(t) = B\sin(bt)$
Here:
$a = 5$
$b = A = B = 4$
$\delta = 0$
$\,t\in [0,\frac{5\pi}4]$
Note: it slows down going around curves
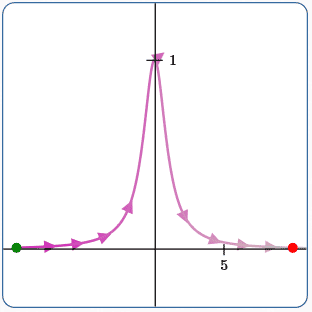
Example (6)
Witch of Agnesi
$x(t) = at$
$\displaystyle y(t) = a/(1+ t^2)$
Here:
$\,a = 1$
$\,t\in [-10,10]$
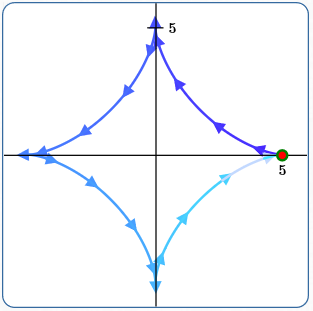
Example (7)
Astroid
$x(t) = a\,\cos^3 t$
$y(t) = a\,\sin^3 t$
Here:
$\,a = 5\,$
$\,t\in [0,2\pi]$
(Start and end points are the same)

Example (8)
After the linked page fully loads, scroll down to look at the equations for $\,x(t)\,$ and $\,y(t)\,.$ Pretty impressive!
Notes about Parametric Equations
A curve that is generated by parametric equations is called a parametric curve.
Parametric equations can describe curves in space (as opposed to in a plane), by adding a third coordinate:
The equation $\,y = mx + b\,$ is an equation that uses parameters, but it's not a parametric equation. The phrase ‘parametric equation’ is typically reserved for situations where coordinates of points are described using parameter(s).
Bézier curves—important in computer graphics and animation (among other things)—are parametric curves.