Even and Odd Functions

Index card: 16ab

Even Functions

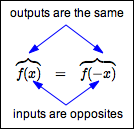
For even functions: when inputs are opposites, the corresponding outputs are the same.

• Recall that $\,x\,$ and $\,-x\,$ are opposites.

  When $\,x\,$ is the input, $\,f(x)\,$ is the output.

  When $\,-x\,$ is the input, $\,f(-x)\,$ is the output.

  For even functions, these two outputs must be equal.

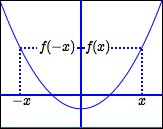
• Note: A function $\,f\,$ is even if and only if the graph of $\,f\,$ is symmetric about the $y$-axis.

• Note:  $\,y = x^2\,,$  $\,y = x^4\,,$  $\,y = x^6\,,$  $\,y = x^8\,,$ etc., are all even functions. Thus, power functions with even powers are even functions! So, the name ‘even’ seems reasonable.

• There are lots of other even functions. For example, $\,y = |x|\,$ and $\,y = \cos(x)\,$ are even functions.

• Is  $\,g(t) = t^2 - t^4\,$  an even function?

  You must investigate $\,g(-t)\,,$ and compare it with $\,g(t)\,,$ as follows:

  $$ \begin{align} \cssId{s28}{g(-t)} &\cssId{s29}{=} \cssId{s30}{(-t)^2 - (-t)^4}\cr &\quad\cssId{s31}{\text{(definition of $\,g\,$; function evaluation)}}\cr\cr &\cssId{s32}{=} \cssId{s33}{t^2 - t^4}\cr &\quad\cssId{s34}{\text{(simplify)}}\cr\cr &\cssId{s35}{=} \cssId{s36}{g(t)}\cr &\quad\cssId{s37}{\text{(definition of $g$)}} \end{align} $$

  Thus, $\,g\,$ is an even function.

Odd Functions

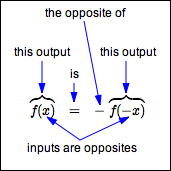
For odd functions: when inputs are opposites, the corresponding outputs are opposites.

• Recall that $\,x\,$ and $\,-x\,$ are opposites.

  When $\,x\,$ is the input, $\,f(x)\,$ is the output.

  When $\,-x\,$ is the input, $\,f(-x)\,$ is the output.

  For odd functions, these two outputs must be opposites.

• Observe that ‘$\,f(x) = -f(-x)\,$’ is equivalent to ‘$\,f(-x) = -f(x)\,$’ (multiply both sides by $\,-1\,$ and switch sides).

  Sometimes, the definition is given using this equivalent characterization.

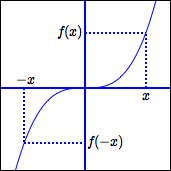
• Note: A function $\,f\,$ is odd if and only if the graph of $\,f\,$ is symmetric about the origin.

• Note:  $\,y = x\,,$  $\,y = x^3\,,$  $\,y = x^5\,,$  $\,y = x^7\,,$  $\,y = x^9\,,$ etc., are all odd functions. Thus, power functions with odd powers are odd functions! So, the name ‘odd’ seems reasonable.

• There are lots of other odd functions. For example, $\,y = \frac{1}{x}\,$ and $\,y = \sin(x)\,$ are odd functions.

• Is  $\,g(x) = x^3 - 1\,$  an odd function?

  That is, are $\,g(-x)\,$ and $\,g(x)\,$ opposites?

  That is, are $\,g(-x)\,$ and $\,-g(x)\,$ equal?

  $$\cssId{s72}{g(-x)} \cssId{s73}{= (-x)^3 - 1} \cssId{s74}{= -x^3 - 1}$$

  Find $\,g(-x)\,$:
  definition of $\,g\,$;  function evaluation.

  $$\cssId{s77}{-g(x)} \cssId{s78}{= -(x^3-1)} \cssId{s79}{= -x^3 + 1}$$

  Find the opposite of $\,g(x)\,$:
  definition of $\,g\,$;  the distributive law.

  Since $\,g(-x)\,$ and $\,-g(x)\,$ are different, $\,g\,$ is not an odd function.

• If an odd function is defined at zero, then its graph must pass through the origin. Why?

  If $\,f\,$ is odd and defined at zero, then:

  $f(x) = -f(-x)$	Requirement for an odd function
  $f(0) = -f(-0)$	Let $\,x = 0$
  $f(0) = -f(0)$	The opposite of zero is zero
  $2f(0) = 0$	Add $\,f(0)\,$ to both sides
  $f(0) = 0$	Divide both sides by $\,2$