Using the Law of Cosines in the SSS Case (& Introduction to the Arccosine Function)

To solve a triangle means to find all the angles and all the side lengths.

The Law of Sines is a valuable tool in solving triangles, but it requires knowing an angle and its opposite side. So, the Law of Sines can't be used as a first step in solving SSS (side-side-side) or SAS (side-angle-side) configurations.

In an earlier section, we saw that the Law of Cosines comes to the rescue! There, an example showed how to use the Law of Cosines in a SAS situation. Here, we'll talk about using the Law of Cosines in a SSS situation.

To do this, some knowledge of the arccosine is required. (The arccosine function will be studied in more detail later on—you just get a basic working knowledge here.)

Introduction to the Arccosine Function

When the Law of Cosines is used in a SSS case (a triangle with sides $\,d\,,$ $\,e\,$ and $\,f\,$ known), then the angle $\,D\,$ (across from side $\,d\,$) is the unknown in the following equation:

$$ \cssId{s12}{d^2 = e^2 + f^2 - 2ef\cos D} $$

Solving for $\cos D\,$ gives:

$$ \cssId{s14}{\cos D = \frac{d^2 - e^2 - f^2}{-2ef}} $$

The right-hand side is just a constant, since $\,d\,,$ $\,e\,$ and $\,f\,$ are all known. For the moment, suppose that this right-hand side evaluates to (say) $\,0.5\,.$ Then, we'd need to solve:

$$ \cssId{s18}{\cos D = 0.5} $$

So the question is:

What angle(s) have cosine equal to $\,0.5\,$?

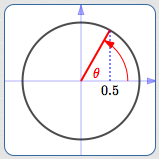
$\theta = 60^\circ\,,$ $\cos\theta = 0.5$

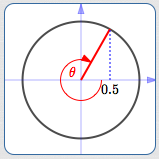
$\theta = -300^\circ\,,$ $\cos\theta = 0.5$

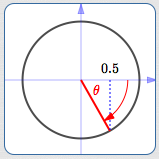
$\theta = -60^\circ\,,$ $\cos\theta = 0.5$

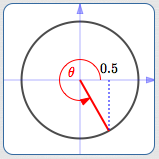
$\theta = 300^\circ\,,$ $\cos\theta = 0.5$

Of course, there are infinitely many: any angle whose terminal point has an $x$-value of $\,0.5\,.$ (Look above and/or below to see a bunch of them.)

$\cos 60^\circ = 0.5$

$\cos(-60^\circ) = 0.5$

$\cos(-300^\circ) = 0.5$

$\cos 300^\circ = 0.5$

$\cos 420^\circ = 0.5$

$\cos(-420^\circ) = 0.5$

$\cos(660^\circ) = 0.5$

$\cos(-1740^\circ) = 0.5$

and so on!!

The arccosine function can be abbreviated as ‘$\,\arccos\,$’, but is still pronounced ‘arc-co-sign’. The arccosine function helps us to ‘undo’ the cosine!

Arccosine is a function: each input has exactly one output. When we ask for $\,\text{arccos}(0.5)\,,$ we can't be given all the angles with a cosine of $\,0.5\,$! We need $\,\text{arccos}(0.5)\,$ to represent exactly one angle. So, which one? Answer: the one between $\,0^\circ\,$ and $\,180^\circ\,$!

That is, by definition:

$$ \begin{align} &\text{arccos}(\color{red}{x})\cr &\qquad = \text{the angle between $\,0^\circ\,$ and $\,180^\circ\,$}\cr &\qquad\qquad\ \text{whose cosine is $\color{red}{x}$} \end{align} $$

So, what exactly is $\,\text{arccos}(x)\,$? Answer: It is the angle between $\,0^\circ\,$ and $\,180^\circ\,$ that has a cosine of $\,x\,.$

So:

$$ \begin{align} &\text{arccos}(\color{red}{0.5})\cr &\qquad = \text{the angle between $\,0^\circ\,$ and $\,180^\circ\,$}\cr &\qquad\qquad\ \text{whose cosine is $\color{red}{0.5}$}\cr &\qquad = 60^\circ \end{align} $$

Arccosine is ‘Safer’ Than Arcsine When Solving Triangles

At this point you've been introduced to both the arcsine and the arccosine.

The arcsine ‘undoes’ the sine. The arccosine ‘undoes’ the cosine. Let's compare them:

$\,\arcsin(x)\,$ is the angle between $\,-90^\circ\,$ and $\,90^\circ\,$ whose sine is $\,x$
$\,\arccos(x)\,$ is the angle between $\,0^\circ\,$ and $\,180^\circ\,$ whose cosine is $\,x$

Ponder these two scenarios:

Scenario #1

You've got an unknown angle in a triangle.
You know its sine is $\,x\,.$
Will $\,\arcsin(x)\,$ always give you the angle you want?

Answer: NO!!

If the unknown angle is acute, then $\,\arcsin(x)\,$ gives us what we want.
If the unknown angle is obtuse, then $\,\arcsin(x)\,$ doesn't give us what we want.
Since the angle is unknown, we likely don't know ahead of time whether it's acute or obtuse.

This is why you must be careful when using Law of Sines to solve a triangle.

Scenario #2

You've got an unknown angle in a triangle.
You know its cosine is $\,x\,.$
Will $\,\arccos(x)\,$ always give you the angle you want?

Answer: YES!!

Angles in triangles are between $\,0^\circ\,$ and $\,180^\circ\,.$
The arccosine always gives an angle between $\,0^\circ\,$ and $\,180^\circ\,.$
And, there's only one angle between $\,0^\circ\,$ and $\,180^\circ\,$ with a given cosine value.

For this reason, when solving triangles:

The Law of Cosines is safer to use than the Law of Sines

Using the Law of Cosines to Solve an SSS Triangle

A triangle has sides of lengths $\,3\,,$ $\,5\,$ and $\,7\,.$ Solve the triangle.

Solution

A quick sketch (above) serves two purposes:

to define notation
to check that you aren't being given an ‘impossible’ triangle

By SSS, the triangle is unique.

The Law of Cosines is the only tool to use when you don't know any angle.

Since the longest side is opposite the biggest angle, $\,D\,$ is the biggest angle. The Law of Cosines is safe to use with big angles, so use it to find $\,D\,$:

$$ \begin{gather} \cssId{s78}{7^2 = 3^2 + 5^2 - 2\cdot 3\cdot 5\cos D}\cr\cr \cssId{s79}{\cos D = \frac{7^2 - 3^2 - 5^2}{-2\cdot 3\cdot 5} = -0.5}\cr\cr \cssId{s80}{D = \arccos(-0.5) = 120^\circ} \end{gather} $$

Mark angle $\,D\,$ on the sketch.

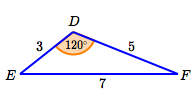
You could use the Law of Cosines again, but the Law of Sines is easier.

A triangle can have at most one obtuse angle, so the remaining angles are acute. Therefore, you can safely use the Law of Sines with either angle. To reinforce good habits, though, use the Law of Sines with the shorter side:

$$ \begin{gather} \cssId{s86}{\frac{\sin 120^\circ}{7} = \frac{\sin F}{3}}\cr\cr \cssId{s87}{\sin F = \frac{3\sin 120^\circ}{7} \approx 0.3712}\cr\cr \cssId{s88}{F = \arcsin(0.3712) \approx 21.79^\circ}\cr\cr\cr \cssId{s89}{E = 180^\circ - 120^\circ - 21.79^\circ = 38.21^\circ} \end{gather} $$

Mark the remaining angles on the sketch.

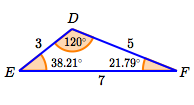
If you've got time, the ‘ultimate check’ is to check the Law of Sines ratios:

$$ \begin{gather} \cssId{s92}{\frac{\sin 120^\circ}{7} \approx 0.1237}\cr\cr \cssId{s93}{\frac{\sin 21.79^\circ}{3} \approx 0.1237}\cr\cr \cssId{s94}{\frac{\sin 38.21^\circ}{5} \approx 0.1237}\cr\cr \end{gather} $$

They agree! Awesome!