Law of Cosines (Part 1)

(This page is Part 1. Click here for Part 2.)

To solve a triangle means to find all the angles and all the side lengths.

The Law of Sines is a valuable tool in solving triangles, but the Law of Sines requires knowing an angle and its opposite side.

Therefore, we need a different tool to begin solving a SSS (side-side-side) or SAS (side-angle-side) configuration.

The Law of Cosines (which can be viewed as a generalization of the Pythagorean Theorem) comes to the rescue!

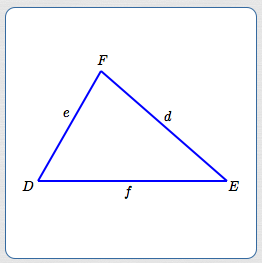
In this section, capital letters are used to denote angles/vertices. Corresponding lowercase letters are used to denote lengths of opposite sides. Thus:

• angle $\,D\,$ is opposite side $\,d\,$
• angle $\,E\,$ is opposite side $\,e\,$
• angle $\,F\,$ is opposite side $\,f\,$

To significantly cut down on words, I say things like:

‘angle $\,D\,$ is opposite side $\,d\,$’

instead of the more correct (but wordier):

‘angle $\,D\,$ is opposite the side of length $\,d\,$’

See more issues about triangle notation here.

Motivation for the Law of Cosines

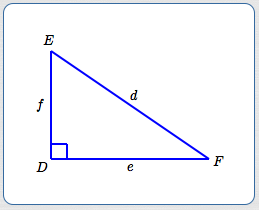
Consider the triangle above. Since $\,D\,$ is a right angle, the well-known Pythagorean Theorem tells us:

Such a beautiful, simple, relationship between the lengths of the sides:

But, what if $\,D\,$ isn't a right angle? Let's investigate.

Keep $\,e\,$ and $\,f\,$ the same, but change angle $\,D\,$:

• Make $\,D\,$ bigger, so it's now an obtuse angle.

  

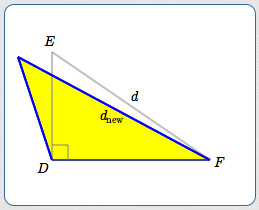
  To compensate, its opposite side needs to get longer:

  $$\cssId{s29}{d_{\text{new}} \gt d}$$

• Make $\,D\,$ smaller, so it's now an acute angle.

  

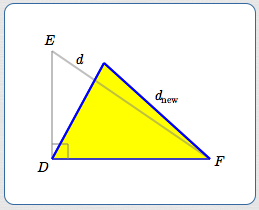
  To compensate, its opposite side needs to get shorter:

  $$\cssId{s32}{d_{\text{new}} \lt d}$$

The Law of Cosines introduces an ‘adjustment’ to the Pythagorean Theorem to account for the change in the length of $\,d\,$!

If $\,D\,$ becomes an obtuse angle, its opposite side gets longer:

$$\cssId{s35}{d_{\text{new}} > d}$$

If $\,D\,$ becomes an acute angle, its opposite side gets shorter:

$$\cssId{s37}{d_{\text{new}} \lt d}$$

THEOREM the Law of Cosines

Consider an arbitrary triangle (see above), where:

• angle $\,D\,$ is opposite a side of length $\,d\,$
• angle $\,E\,$ is opposite a side of length $\,e\,$
• angle $\,F\,$ is opposite a side of length $\,f\,$

Then:

$$ \cssId{s45}{d^2 = e^2 + f^2 - 2ef\cos D} $$

Notes on the Law of Cosines

Three Applications of the Law of Cosines in Every Triangle

Since there are three sides in every triangle, there are three applications of the Law of Cosines in every triangle. Here are the other two versions:

Verbalizing the Law of Cosines

In any triangle, the square of a side is the sum of the squares of the other two sides, minus twice the product of the other two sides times the cosine of the included angle.

Quite a mouthful! Here are the words, ‘attached’ to the formula:

The Adjustment

Here is the ‘adjustment’ in the Law of Cosines:

When the adjustment is positive, then $\,d^2\,$ is bigger than it would be, if it were opposite a $\,90^\circ\,$ angle. A bigger value of $\,d^2\,$ means a bigger value of $\,d\,.$

Similarly, when the adjustment is negative, then $\,d^2\,$ is smaller than it would be, if it were opposite a $\,90^\circ\,$ angle. A smaller value of $\,d^2\,$ means a smaller value of $\,d\,.$

When $\,D = 90^\circ\,,$ the Adjustment is Zero

When $\,D = 90^\circ\,$ (that is, in a right triangle), we have $\,\cos D = \cos 90^\circ = 0\,.$ In this case, the adjustment is zero, and the Law of Cosines reduces to the Pythagorean Theorem.

When $\,D\,$ is Obtuse, the Adjustment is Positive

For angles $\,D\,$ strictly between $\,90^\circ\,$ and $\,180^\circ\,,$ we have $\,\cos D \lt 0\,.$ Since $\,e\,$ and $\,f\,$ (side lengths) are strictly positive, this means that:

Since the adjustment is positive, $\,d\,$ is longer than it would be, if it were opposite a $\,90^\circ\,$ angle. Take another look at the image from the motivation!

When $\,D\,$ is Acute, the Adjustment is Negative

For angles $\,D\,$ strictly between $\,0^\circ\,$ and $\,90^\circ\,,$ we have $\,\cos D \gt 0\,.$ Since $\,e\,$ and $\,f\,$ (side lengths) are strictly positive, this means that:

Since the adjustment is negative, $\,d\,$ is shorter than it would be, if it were opposite a $\,90^\circ\,$ angle. Take another look at the image from the motivation!