Introduction to Polygons

Due to math content, this page has special requirements (including JavaScript) for full functionality.
With your current viewing scenario, it is not appearing and behaving as it is supposed to!
Please visit Dr. Carol J.V. Fisher's Homepage to learn what this site has to offer.
Watch the "Welcome" video to get started—hope to see you back here soon!

Dr. Carol J.V. Fisher's Homepage

For this exercise, you need ♥ INTERNET EXPLORER 6.0 and above, with MathPlayer installed.♥

INTRODUCTION TO POLYGONS

Jump right to the exercises!

Here are additional illustrations of polygons: http://www.mathleague.com/help/geometry/polygons.htm

DEFINITION: A polygon is a closed figure in a plane made by joining line segments,
where each line segment intersects exactly two others.
Note: Strictly speaking, a polygon does not include its interior (the space inside the polygon).


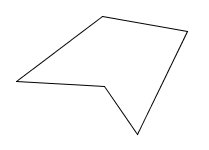a polygon	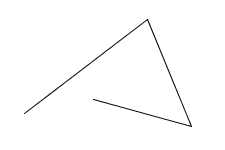not closed; not a polygon	not made of line segments; not a polygon	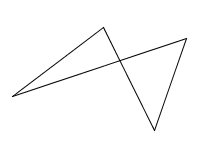line segment intersects more than two others; not a polygon

Polygons are usually classified according to how many sides they have:

DEFINITIONS:

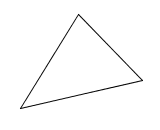A *triangle* is a polygon with 3 sides.		A *heptagon* is a polygon with 7 sides.
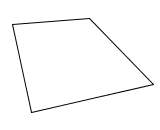A *quadrilateral* is a polygon with 4 sides.		An *octagon* is a polygon with 8 sides.
A *pentagon* is a polygon with 5 sides.		A *nonagon* is a polygon with 9 sides.
A *hexagon* is a polygon with 6 sides.		A *decagon* is a polygon with 10 sides.

More generally, a polygon with n sides can be called an n-gon.
For example, a polygon with 27 sides can be called a 27-gon.

DEFINITION: The vertices of a polygon are the points where its sides intersect.
The singular form of vertices is vertex.
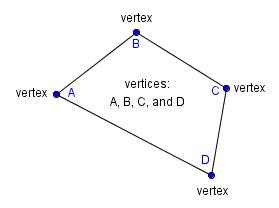
vertex; vertices

NAMING POLYGONS:
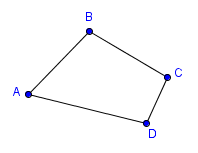
When naming polygons, the vertices must be listed in consecutive order.
For example, the polygon at right below could be named:
polygon ABCD (start with A, move clockwise);
polygon ADCB (start with A, move counter-clockwise);
polygon BCDA (start with B, move clockwise);
polygon BADC (start with B, move counter-clockwise);
polygon CDAB (start with C, move clockwise);
polygon CBAD (start with C, move counter-clockwise);
polygon DABC (start with D, move clockwise);
polygon DCBA (start with D, move counter-clockwise).

More generally, when naming an n-gon, there are n choices for listing the first vertex.
Then, there are 2 choices for the next vertex (moving clockwise or counterclockwise).
The remaining vertices are then completely determined.
Thus, there are 2n choices for the polygon name.

DEFINITION: A regular polygon is a polygon whose sides all have the same length, and whose angles are all the same.


a regular triangle	a regular quadrilateral (a square)	a regular pentagon	a regular hexagon


a regular heptagon	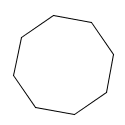a regular octagon	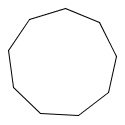a regular nonagon	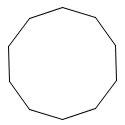a regular decagon

DEFINITION: A rectangle is a quadrilateral whose angles are all right angles.

DEFINITION: A square is a rectangle with all sides of equal length.

Note: Every square is a rectangle.
However, not every rectangle is a square.
That is, there exist rectangles that are not squares.


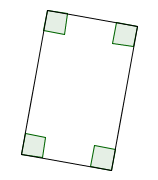
each of these is a rectangle, but NOT a square

On this exercise, you will not key in your answers.
However, you can check to see if your answer is correct.