• Jump right to the exercises!
• You may want to review:
  Beginning Terminology: Points, Lines, and Planes

DEFINITION and NOTATION line segment

A line segment is a part of a line that has finite length.
The line segment with endpoints $\,A\,$ and $\,B\,$ will be denoted by [beautiful math coming... please be patient] $\,\overline{AB}\,$ or $\,\overline{BA}\,$.

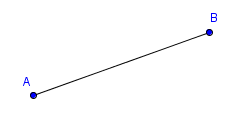
The geometric figure [beautiful math coming... please be patient] $\overline{AB}\,$ can be read aloud as ‘segment $\,A\,B\,$’.
Notice that $\overline{AB}\,$ is precisely the same set of points as $\overline{BA}\,$.

DEFINITION and NOTATION ray

A ray is a half-line, together with its endpoint.

If a ray has endpoint $\,A\,$, and if $\,B\,$ is any other point on the half-line,
then the ray will be denoted by [beautiful math coming... please be patient] $\,\overrightarrow{AB}\,$.

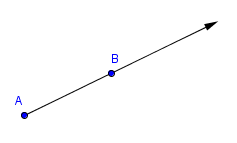$\overrightarrow{AB}$

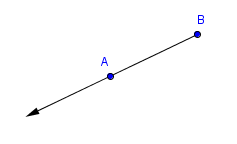[beautiful math coming... please be patient] $\overrightarrow{BA}$

The geometric figure [beautiful math coming... please be patient] $\overrightarrow{AB}\,$ can be read aloud as ‘ray $\,A\,B\,$’.
The endpoint is written first and is read first.

In particular, notice that [beautiful math coming... please be patient] $\,\overrightarrow{AB}\,$ and $\,\overrightarrow{BA}\,$ have different endpoints.

DEFINITION and NOTATION angle

An angle is a pair of rays that share a common endpoint.
The rays are called the sides of the angle.
The common endpoint is called the vertex of the angle.

If there is only one angle with vertex $\,V\,$,
then the angle can be denoted by the simple name $\,\angle V\,$.

Sometimes, a slightly more complicated notation is needed for angles.
If $\,A\,$ is a point on one side, $\,V\,$ is the vertex, and $\,B\,$ is a point on the other side, then the angle can be denoted by $\,\angle AVB\,$ or $\,\angle BVA\,$.

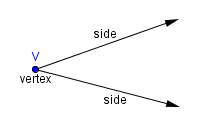
[beautiful math coming... please be patient] $\angle V$

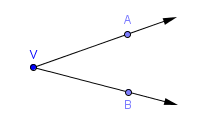
$\angle AVB$

A protractor is a device that is used to measure and draw angles.

a protractor

Animation: Using a Protractor to Measure Angles Animation: Using a Protractor to Draw an Angle Click here for a protractor worksheet

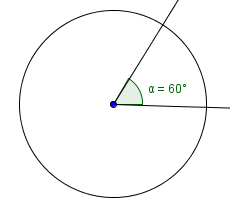
The measure of an angle is a number that specifies how ‘wide’ the angle is.

Angles are often measured in degrees.
Take one complete revolution (once around a circle), and divide it into $\,360\,$ equal parts.
Each part is one degree.
Thus, one degree is [beautiful math coming... please be patient] $\,\frac{1}{360}\,$ of a complete revolution.

TWO VIEWS OF A ONE-DEGREE ANGLE;
$\,\frac{1}{360}\,$ of a complete revolution

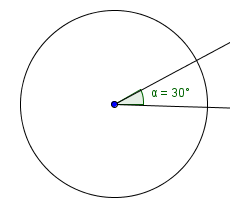
The notation [beautiful math coming... please be patient] $\,45^{\circ}\,$ denotes $\,45\,$ degrees.
You should be comfortable recognizing some common degree measures:   $\,30^{\circ}\,$, $\,45^{\circ}\,$, $\,60^{\circ}\,$, $\,90^{\circ}\,$

DEFINITION and NOTATION right angle

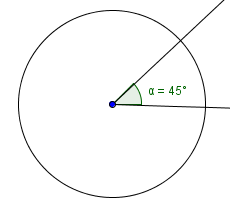
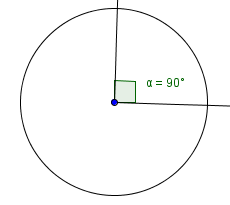
A right angle is a $\,90^{\circ}\,$ angle.

Right angles are marked in a diagram using this little square (since a square has $\,90^{\circ}\,$ angles):

Recall that geometric figures are collections of points; they are subsets of space.
For example, this fancy letter ‘$\,\mathcal{G}\,$’ is a geometric figure (although not one that is commonly discussed)!
Geometric figures are mathematical expressions—they are mathematical objects of interest.
As with any new expression, you need to develop tools for working with them—for asking and answering questions about them.

Already, several important geometric figures have been introduced: points, lines, planes, line segments, rays, and angles.
Depending on the geometric figures being considered, you might ask different questions.
For example, you might ask if two line segments have the same length; or, you might ask if two angles have the same degree measure.
In these questions, we are ‘comparing’ geometric figures that happen to be of the same type—two line segments; two angles.

Thus, you might find yourself asking—is it possible to ‘compare’ arbitrary geometric figures?
In particular, should we make sense of what it might mean to say that two geometric figures are ‘the same’ or ‘equal’?
We did this for numbers: two numbers are equal when they correspond to the same position on a number line.
We did this for matrices: two matrices are equal when they have the same size, and corresponding elements are equal.
We did this for ordered pairs: two ordered pairs are equal when their first coordinates are equal, and their second coordinates are equal.

If geometric figures are residing in a coordinate system—where we have a way to specify locations of points—
then perhaps we could define two geometric figures to be ‘equal’ when they consist of precisely the same set of points.
With this type of definition:

• a point located at the top of a page would not be ‘equal to’ a point at the bottom of the page,
  because they would reside at different locations in the coordinate system
• a line segment of length $\,2\,$ in a horizontal orientation wouldn't be ‘equal to’ a line segment of length $\,2\,$ in a vertical orientation,
  because they would consist of different sets of points in the coordinate system

Although this type of ‘equality’ might be useful in some situations, it is instead
a very different method of comparison that becomes of the utmost importance in geometry—
a method that is completely independent of the location of an object in space,
and instead has only to do with how points are positioned relative to each other.

We won't call this method of comparison ‘equality’ of geometric figures,
because we certainly don't want to get ourselves confused with any coordinate system sense of ‘equality’.
Instead, we'll talk about geometric figures being congruent, which is introduced next:

An extremely important concept for comparing geometric figures is congruence.
Two geometric figures are congruent if they have exactly the same size and shape.
Congruent figures can be superimposed one over the other, and they will match up perfectly.
The symbol that is used for congruence is $\,\cong \,$.

Note the following:

• In mathematics, the word distinct is used to mean different.
• CONGRUENCE OF POINTS, LINES, and PLANES:
  All points are congruent.
  That is, for all points [beautiful math coming... please be patient] $\,A\,$ and $\,B\,$, $\,A\cong B\,$.
  
  All lines are congruent.
  That is, for all distinct points $\,A\,$ and $\,B\,$,
  and for all distinct points $\,C\,$ and $\,D\,$,
  $\,\overleftrightarrow{AB} \cong \overleftrightarrow{CD}\,$   (read aloud as:   ‘line $\,A\,B\,$ is congruent to line $\,C\,D\,$’)
  
  All planes are congruent.
  That is, for all distinct noncollinear points $\,A\,$, $\,B\,$, and $\,C\,$,
  and for all distinct noncollinear points $\,D\,$, $\,E\,$, and $\,F\,$,
  $\,ABC\cong DEF\,$   (read aloud as:   ‘plane $\,A\,B\,C\,$ is congruent to plane $\,D\,E\,F\,$’)
• CONGRUENCE OF LINE SEGMENTS:
  For distinct points $\,A\,$ and $\,B\,$,
  [beautiful math coming... please be patient] $\,\overline{AB}\cong \overline{BA}\,$   (read aloud as:   ‘line segment $\,A\,B\,$ is congruent to line segment $\,B\,A\,$’)
  
  Indeed, you can decide if two line segments are congruent by comparing their lengths:
  • if two line segments have the same length, then they are congruent
  • if two line segments are congruent, then they have the same length
  Recall that these previous two sentences can be abbreviated as:
  Two lines segments are congruent if and only if they have the same length.
  If you need to review if and only if and the concept of mathematical equivalence, then click here.