Parallelograms and Negating Sentences
By definition, a parallelogram is a quadrilateral where both pairs of opposite sides are parallel.
If you're trying to show that a quadrilateral is a parallelogram, however, then using the definition isn't always the easiest approach.
There are many different ways that a quadrilateral can be determined to be a parallelogram. Five of the most common ways are explored in this section.
- $Q\,$ is a parallelogram (i.e., both pairs of opposite sides are parallel)
- the diagonals of $\,Q\,$ bisect each other
- both pairs of opposite sides are equal
- both pairs of opposite angles are equal
- one pair of opposite sides are both parallel and equal
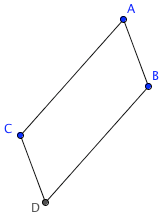$\overline{AB}\parallel \overline{CD}$and
$\overline{AC}\parallel \overline{BD}$
bisect each other
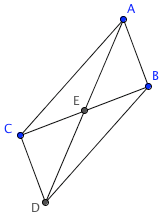$AE = ED$and
$CE = EB$
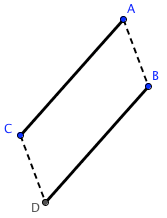$AB = CD$and
$AC = BD$
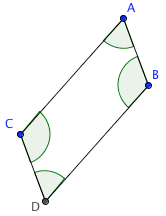$m\angle A = m\angle D$and
$m\angle B = m\angle C$
$\overline{AC}\parallel \overline{BD}$and
$AC = BD$
If you've been progressing through these Topics in Geometry, then you have all the tools you need to prove the previous theorem.
You could use a chain of implications together with a variety of prior results. There are many routes you can take—here's one possibility:
| both pairs of opposite sides parallel | $\Rightarrow$ | both pairs of opposite angles are equal |
| $\Rightarrow$ | one pair of opposite sides are both parallel and equal | |
| $\Rightarrow$ | both pairs of opposites sides are equal | |
| $\Rightarrow$ | the diagonals bisect each other | |
| $\Rightarrow$ | both pairs of opposite sides are parallel |
Hint: You may need all these prior results:
Logical Skills for Negating Sentences
You should be able to negate each of the statements in the theorem above, and phrase these negations in a variety of ways.
The skills for negating ‘and’ and ‘or’ sentences were explored in Logical Equivalences and Practice with Truth Tables. They are reviewed here for your convenience:
How can a sentence ‘$A\text{ and }B\,$’ be false? The only time an ‘and’ sentence is true is when both subsentences are true. Therefore, an ‘and’ sentence is false when at least one of the subsentences is false.
Precisely, the truth table below shows that: $$ \begin{gather} \cssId{s53}{\text{not}(A\text{ and } B)}\cr \cssId{s54}{\text{ is equivalent to }}\cr \cssId{s55}{\bigl((\text{not }A)\text{ or }(\text{not }B)\bigr)} \end{gather} $$
| $A$ | $B$ | $A\text{ and }B$ | $\text{not}(A \text{ and }B)$ |
| T | T | T | F |
| T | F | F | T |
| F | T | F | T |
| F | F | F | T |
| $\text{not } A$ | $\text{not } B$ | $(\text{not }A) \text{ or } (\text{not }B)$ |
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | T |
How can a sentence ‘$A\text{ or }B\,$’ be false? An ‘or’ sentence is false only when both of the subsentences are false.
Precisely, the truth table below shows that: $$ \begin{gather} \cssId{s59}{\text{not}(A\text{ or }B)}\cr \cssId{s60}{\text{ is equivalent to }}\cr \cssId{s61}{\bigl((\text{not }A)\text{ and }(\text{not }B)\bigr)} \end{gather} $$
| $A$ | $B$ | $A \text{ or }B$ | $\text{not}(A \text{ or }B)$ |
| T | T | T | F |
| T | F | T | F |
| F | T | T | F |
| F | F | F | T |
| $\text{not }A$ | $\text{not }B$ | $(\text{not }A) \text{ and }(\text{not }B)$ |
| F | F | F |
| F | T | F |
| T | F | F |
| T | T | T |
Negating ‘For all’ and ‘There exist’ Sentences
Next, consider a sentence of the form:
‘$\,\text{For all }x\text{, }P\ $’
To understand a (true) sentence of this form, think of a population where each member has property $\,P\,,$ as shown below:
What does it mean to say that the sentence ‘$\,\text{For all }x\text{, }P\ $’ is not true? It means that at least one member of the population doesn't have property $\,P\,,$ like this:
Of course, it could certainly be true that more than one member of the population doesn't have property $\,P\,,$ like this:
Precisely: $$ \begin{gather} \cssId{s71}{\text{not}(\text{For all }x\text{, }P\,)}\cr \cssId{s72}{\text{ is equivalent to }}\cr \cssId{s73}{\text{There exists }\,x\,\text{ such that }(\text{not }P\,)} \end{gather} $$
Similar reasoning shows that: $$ \begin{gather} \cssId{s75}{\text{not}(\text{There exists }\ x\ \text{ such that }P\,)}\cr \cssId{s76}{\text{ is equivalent to }}\cr \cssId{s77}{\text{For all }x\text{, }(\text{not }P\,)} \end{gather} $$
Negating the Statements in the ‘Equivalent Characterizations of a Parallelogram’ Theorem
Here's an example of applying the negation tools:
- Negate: ‘Both pairs of opposite sides are parallel.’
- Rephrase as a ‘for all’ sentence: For all opposite sides $\,x\,$ and $\,y\,,$ $\,x\parallel y\,.$
- Negate the ‘for all’ sentence: There exist opposite sides $\,x\,$ and $\,y\,$ such that $\,x\not\parallel y\,.$
- Rephrase the negation as an English sentence: There exists a pair of opposite sides that are not parallel.
These are all negations of: $\,Q\,$ is a parallelogram (i.e., both pairs of opposite sides are parallel)
- $Q\,$ is not a parallelogram
- it is not true that both pairs of opposite sides are parallel
- at least one pair of opposite sides are not parallel
- there exists a pair of opposite sides that are not parallel
These are all negations of: the diagonals of $\,Q\,$ bisect each other
- it is not true that the diagonals of $\,Q\,$ bisect each other
- at least one diagonal of $\,Q\,$ is not bisected at the point of intersection of the diagonals
- there exists a diagonal of $\,Q\,$ that is not bisected at the point of intersection of the diagonals
These are all negations of: both pairs of opposite sides are equal
- it is not true that both pairs of opposite sides are equal
- at least one pair of opposite sides are not equal
- there exists a pair of opposite sides that are not equal
These are all negations of: both pairs of opposite angles are equal
- it is not true that both pairs of opposite angles are equal
- at least one pair of opposite angles are not equal
- there exists a pair of opposite angles that are not equal
Notice that ‘one pair of opposite sides are both parallel and equal’ can be re-phrased as ‘at least one pair of opposite sides are both parallel and equal’ or ‘there exists a pair of opposite sides that are both parallel and equal’.
These are negations of: one pair of opposite sides are both parallel and equal
- it is not true that one pair of opposite sides are both parallel and equal
- each pair of opposite sides are either not parallel or not equal