Interior and Exterior Angles in Polygons

You may want to review:  Introduction to Polygons

We'll start by talking about triangles, and then extend the ideas to any polygon.

Recall that lowercase Greek letters are commonly used to denote angles: this lesson uses $\,\alpha\,$ (alpha), $\,\beta\,$ (beta), and $\,\gamma\,$ (gamma).

It's easy to see that the sum of the angles in any triangle is $\,180^{\circ},$ as follows:

• First, start with a right triangle (i.e., a triangle that has a $\,90^{\circ}\,$ angle).
• Make it into a rectangle, as shown below, to see that $\,\alpha +\beta = 90^{\circ}\,.$
• Thus, in any right triangle, the remaining two angles sum to $\,90^{\circ}\,.$

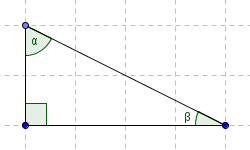Start with a right triangle ...

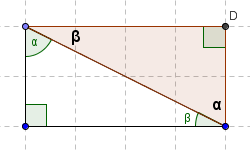... and make it into a rectangle

If you have trouble seeing the rectangle that is formed above, then study the following, paying attention to angle $\,\alpha \,$:

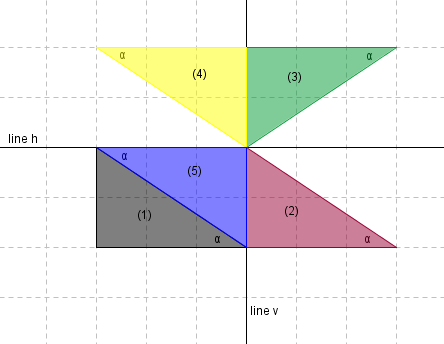
• Start with triangle (1).
• Slide it to the right, to get (2).
• Reflect about the horizontal line $\,h\,,$ to get (3).
• Reflect about the vertical line $\,v\,,$ to get (4).
• Slide it down, to get (5).

Now, consider any triangle. Drop a perpendicular, as shown below, bringing two right triangles into the picture. (Choose a vertex so that the perpendicular is inside the triangle; such a vertex always exists.)

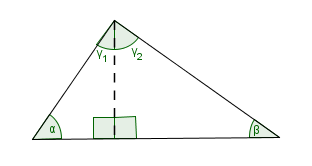
Thus, we have: $$\cssId{s28}{\alpha + \gamma_1 =90^{\circ}}\ \cssId{s29}\ \,{\text{and}}\ \ \cssId{s30}{\beta + \gamma_2 = 90^{\circ}}$$ Together, $$\cssId{s32}{\alpha + \gamma_1 + \gamma_2 + \beta = 180^{\circ}}\,,$$ and so we have:

A quick note about terminology:  you can't really ‘sum’ angles. Angles are geometric figures, and we don't ‘add’ geometric figures. When we talk about adding angles, it is understood that we're adding the measures of the angles.

Not only can we explore the interior (inside) angles of polygons, but we can also explore exterior angles:

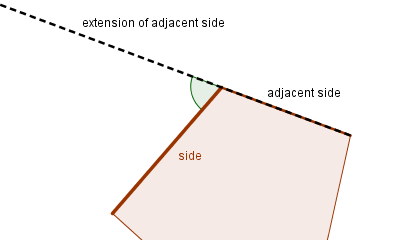
Although two (equal) exterior angles can be drawn at each vertex of a polygon, when we talk about summing the exterior angles of a polygon, we agree to include only one exterior angle at each vertex.

For a triangle with interior angles $\,\alpha \,,$ $\,\beta \,,$ and $\,\gamma \,,$ we have the following: $$ \cssId{s53}{(\alpha + \alpha_{\text{ext}})} \cssId{s54}{+ (\beta + \beta_{\text{ext}})} \cssId{s55}{+ (\gamma + \gamma_{\text{ext}})} \cssId{s56}{= 3(180^{\circ})} $$

Regrouping gives: $$ \cssId{s58}{(\alpha +\beta +\gamma )} \cssId{s59}{+ (\alpha_{\text{ext}} + \beta_{\text{ext}} + \gamma_{\text{ext}})} \cssId{s60}{= 3(180^{\circ})} $$

Since the sum of the (interior) angles of the triangle is $\,180^{\circ}\,,$ it follows immediately that: $$ \cssId{s63}{\alpha_{\text{ext}} + \beta_{\text{ext}} + \gamma_{\text{ext}}} \cssId{s64}{= 2(180^{\circ})} \cssId{s65}{= 360^{\circ}} $$

Thus we have the following:

Walking Around the Perimeter of a Polygon—How Much Do You Turn?

Indeed, you can think about the sum of the exterior angles in the following way. Walk around the perimeter of the triangle above in a counter-clockwise direction. (If we had labeled the other exterior angle at each vertex, you'd walk in the clockwise direction.)

At each vertex, you stop and pivot—you are turning an amount that is equal to an exterior angle! When you reach your starting point, you are facing in exactly the same direction that you started, so you have turned through a total of $\,360^{\circ}$—one complete revolution! This is a nice way to think of why the exterior angles should sum to $\,360^{\circ}\,.$

(Try applying this thought process to the exterior angles in a more general polygon! Can you make a conjecture?)

Sum of Interior Angles in Arbitrary Polygons

The interior angles of any polygon always sum to a constant value, which depends only on the number of sides.

This is easy to see in many cases—take a polygon with $\,n\,$ sides, and divide it into $\,n-2\,$ triangles, as shown below.

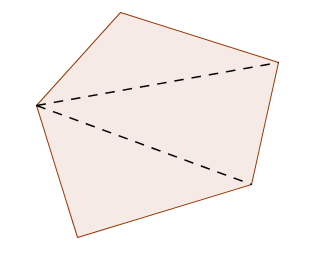
Thus, the sum of the interior angles is $\,(n-2)(180^{\circ})\,.$

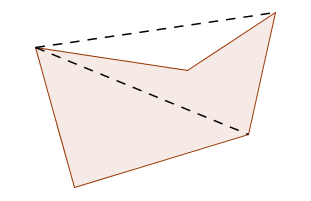
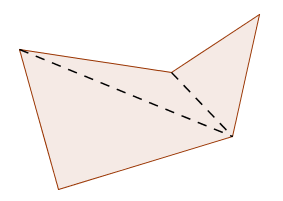
If the polygon ‘caves in’ then this method may break down, as illustrated in the first sketch below. The result is still true—it's just harder to prove!

You can explore interior and exterior angles of polygons at these excellent links:

• interior angle exploration
• exterior angle exploration

(Be patient; they may take a few minutes to load. They'll open in a new window.)