3.3 Designing and Improving Filters

Introduction

The previous section investigated the problem: given a symmetric nonrecursive filter, find its transfer function. The current section shows how to go from a desired transfer function to a symmetric nonrecursive filter. The Fourier series of the desired transfer function plays an important role in this process.

Complex Fourier series

Continuous Fourier series results were reviewed in Section $1.6$. For the current purpose, it is easiest to employ the equivalent complex form of the Fourier series. The relevant results are summarized below. The interested reader is referred to [Ham, $95$–$99$] for additional information.

Complex Fourier Series

Let $\,g\,$ be a periodic real-valued function of one real variable. Suppose that $\,g\,$ is piecewise continuous on $\,\Bbb R\,,$ and has fundamental period $\,P\,.$

The complex Fourier series of $\,g\,$, denoted by $\,\text{Four}(g)\,,$ is the infinite sum

$$ \text{Four}(g)(t) := \sum_{k=-\infty}^\infty C_k\,e^{i\frac{2\pi kt}P}\ , $$

where:

$$ C_k = \frac 1P\int_P e^{-i\frac{2\pi kt}P}\,g(t)\,dt $$

The coefficients $\,C_k\,$ are related to the coefficients $\,a_k\,$ and $\,b_k\,$ by:

$$ \begin{align} C_k &= \frac{a_{(-k)} + ib_{(-k)}}2\ \ \text{for}\ \ k\lt 0\ ,\cr\cr C_0 &= \frac{a_0}2\ ,\cr\cr C_k &= \frac{a_k - ib_k}2\ \ \text{for}\ \ k\gt 0 \end{align} $$
If $\,g\,$ is even, then all $\,C_k\,$ are real, and $\,C_k = C_{-k}\,$ for all $\,k$

If $\,g\,$ is an even function ($\,g(-t) = g(t)\,$ for all $\,t\,$), then $\,b_k = 0\,$ for $\,1\le k\lt \infty\,,$ and hence:

$$ C_k = \cases{ \frac{a_{(-k)}}2 & \text{for}\ \ k\lt 0\cr\cr \frac{a_k}2 & \text{for}\ \ k\ge 0 } $$

In particular, if $\,g\,$ is even, then all values of $\,C_k\,$ are real numbers, and $\,C_k = C_{(-k)}\,$ for all integers $\,k\,.$

Rewriting the transfer function $\,\tilde H$

In order to compare a transfer function $\,\tilde H\,$ (as a function of cyclic frequency) with its complex Fourier series representation, it is rewritten as follows:

$$ \begin{align} &\tilde H(f)\cr\cr &\quad := \sum_{k=-K}^K c_k\,e^{-i2\pi kf\Delta T}\cr\cr &\quad = \sum_{\ell = K}^{-K} c_{(-\ell)}\,e^{i2\pi \ell f \Delta T}\ \ (\ell := -k)\cr\cr &\quad = \sum_{k=-K}^K c_{(-k)}\,e^{i2\pi kf\Delta T} \tag{1} \end{align} $$

Recall from the previous section that $\,\tilde H\,$ has period $\,\frac 1{\Delta T}\,.$ Therefore, the complex Fourier series for $\,\tilde H\,$ is given by:

$$ \begin{align} &\text{Four}(\tilde H)(f)\cr\cr &\quad = \sum_{k=-\infty}^{\infty} C_k\,e^{i\frac{2\pi kf}{1/\Delta T}}\cr\cr &\quad = \sum_{k=-\infty}^\infty C_k\,e^{i2\pi kf\Delta T}\ \ \tag{2} \end{align} $$

By comparing ($1$) and ($2$), it is apparent that the truncated Fourier series will approximate the transfer function, provided that $\,C_k = c_{(-k)}\,$ for $\,k = -K,\ldots,K\,.$

The procedure for finding filter coefficients from a given (desired) transfer function is summarized next:

Procedure: Finding filter coefficients from a given transfer function; extend $\,\tilde H$
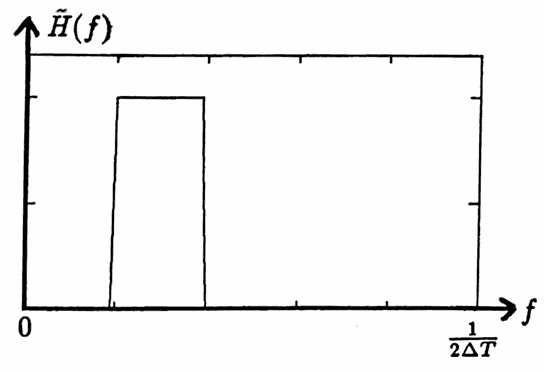
  • Let $\,\Delta T\,$ be a given positive number, representing the uniform spacing in the time list of a data set to be processed. Let $\,\tilde H\,$ denote a desired transfer function on the interval of frequencies $\,[0,\frac 1{2\Delta T}]\,.$

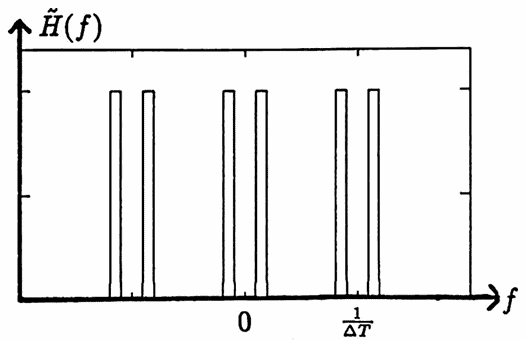
  • Extend $\,\tilde H\,$ to $\,[-\frac 1{2\Delta T},\frac 1{2\Delta T}]\,$ via:

    $$ \tilde H(-t) = \tilde H(t)\ \ \text{for}\ \ t\in [0,\frac 1{2\Delta T}] $$

    (See the diagram below.) Call this extension by the same name.

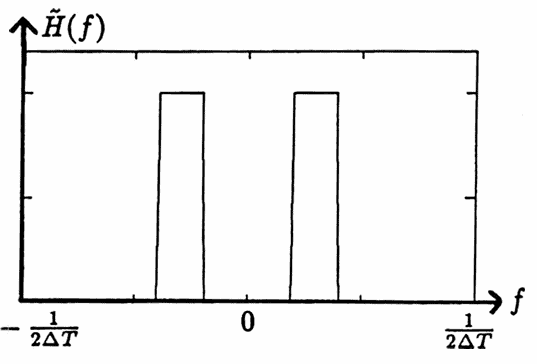
a transfer function extending the transfer function
The extension is an even function

  • Extend $\,\tilde H\,$ periodically to all of $\,\Bbb R\,.$ (See the diagram below.) That is, define

    $$ \tilde H\left( t + k\bigl( \frac 1{\Delta T} \bigr) \right) := \tilde H(t) $$

    for all integers $\,k\,,$ and for all $\,t \in [-\frac 1{2\Delta T},\frac 1{2\Delta T}]\,.$ Call this extension by the same name. The resulting function $\,\tilde H\,$ is even, with fundamental period $\,\frac 1{\Delta T}\,.$

Computing $\,C_k$

  • Since $\,\tilde H\,$ is even, its complex Fourier series coefficients $\,C_k\,$ are real numbers, and $\,C_k = C_{(-k)}\,$ for all integers $\,k\,.$ For $\,k\ge 0\,,$

    $$ C_k = \frac{a_k}2\ , $$

    where

    $$ \begin{align} a_k &=\frac 2P\int_P \tilde H(f)\cos\frac{2\pi kf}P\,df\ \ \text{(see $\S$1.6)}\cr\cr &= 2\Delta T\int_{-\frac 1{2\Delta T}}^{\frac 1{2\Delta T}} \tilde H(f)\cos(2\pi kf\Delta T)\,df\cr &\qquad\qquad\qquad \text{(since $\,P = \frac 1{\Delta T}\,$)}\cr\cr &= 4\Delta T\int_0^{\frac 1{2\Delta T}} \tilde H(f)\cos(2\pi kf\Delta T)\,df\cr &\qquad\qquad\qquad \text{(since $\,\tilde H\,$ is even)}\tag{3} \end{align} $$
Computing the filter coefficients

  • For a positive integer $\,K\,,$ the coefficients $\,c_k\,$ given by

    $$ c_k = c_{-k} = C_k\ \ \text{for}\ \ k = 0,\ldots,K $$

    will give a symmetric nonrecursive filter

    $$ f_n = \sum_{k=-K}^K c_k\,y_{n-k} $$

    with a transfer function that approximates $\,\tilde H(f)\,.$ In general, the greater the value of $\,K\,,$ the better the approximation.

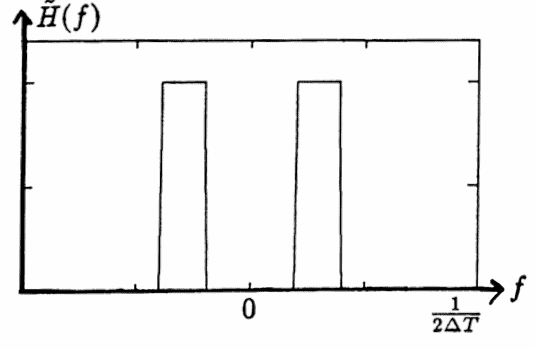
a transfer function extending the transfer function periodically to the real numbers
EXAMPLE: Designing a band-pass filter

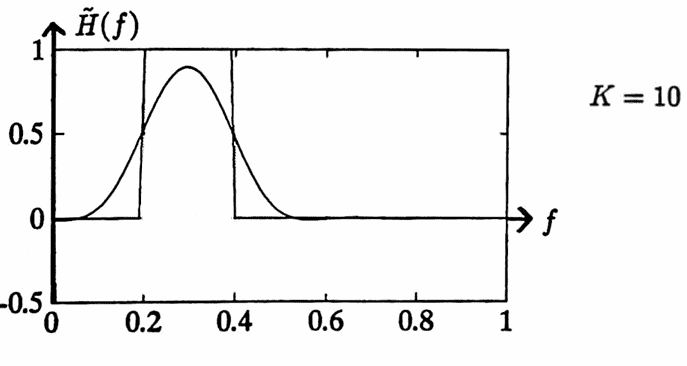
The procedure just described is illustrated next. Let $\,\Delta T = 0.5\,,$ so that $\,\frac 1{2\Delta T} = 1\,.$ A transfer function is desired that will pass the frequencies in an interval $\,[d-\delta\,,\,d+\delta] \subset [0,\frac 1{2\Delta T}]\,,$ and suppress all other frequencies. Such a filter is called a band-pass filter. The desired transfer function is shown below on $\,[0,\frac 1{2\Delta T}]\,.$

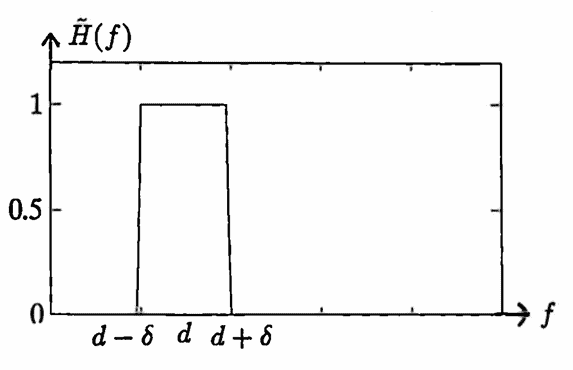
a band-pass filter

Using ($3$):

$$ \begin{align} a_k &= 4\Delta T\int_0^{\frac 1{2\Delta T}} \tilde H(f)\,\cos(2\pi kf\Delta T)\,df\cr\cr &= 4(0.5)\int_0^1 \tilde H(f)\,\cos(2\pi kf(0.5))\,df\cr\cr &= 2 \int_{d-\delta}^{d+\delta} (1)\cos(k\pi f)\,df\cr\cr &= \frac 2{k\pi}[\sin(k\pi(d+\delta)) - \sin(k\pi(d-\delta))]\ ,\ \ \text{for}\ \ k\gt 0 \end{align} $$

Also:

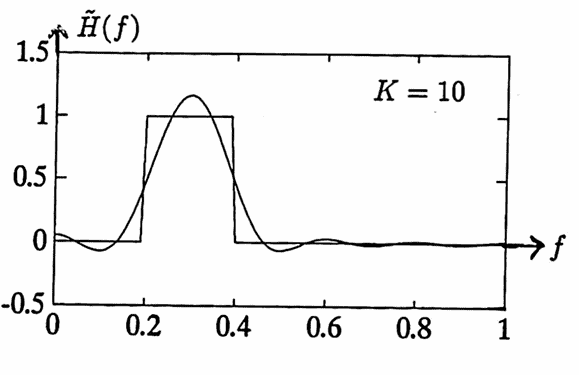
$$ \begin{align} a_0 &= 4\Delta T\int_{d-\delta}^{d+\delta} (1)\,df\cr\cr &= 4(0.5)(2\delta) = 4\delta \end{align} $$

Let $\,d = 0.3\,,$ $\,\delta = 0.1\,,$ and $\,K = 10\,.$ The resulting symmetric nonrecursive filter has coefficients:

$$ \begin{align} &(c_0,c_1,\ldots,c_{10})\cr\cr &\quad = \bigl( \frac{a_0}2,\frac{a_1}2,\ldots,\frac{a_{10}}2 \bigr)\cr\cr &\quad \approx (0.2,\,0.1156,\,-0.0578,\,-0.1633,\cr &\qquad -0.1225,\,0\,,0.0816,\,0.0700,\cr &\qquad 0.0145,\,-0.0128,\,0) \end{align} $$

The transfer function for this filter is shown below, superimposed with the ‘ideal’ transfer function.

transfer function with the 'ideal' transfer function, K = 10
$K = 20$

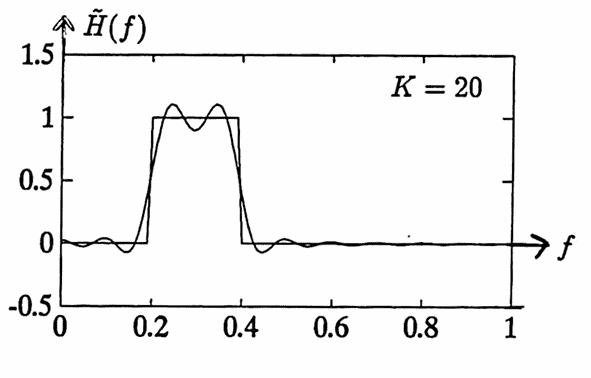
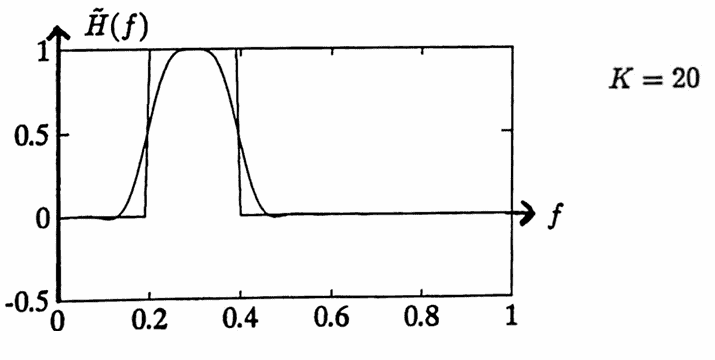
Now, increase $\,K\,$ to $\,20\,,$ keeping all other parameters the same. The transfer function of the resulting symmetric nonrecursive filter is shown below, superimposed with the ‘ideal’ transfer function.

transfer function with the 'ideal' transfer function, K = 20

The ‘ripples’ that appear in the transfer functions can be ‘smoothed’ by a process called Lanczos smoothing.

Lanczos is credited with observing that the ‘ripple’ in a truncated Fourier series has approximately the period of the last term kept in the series. He argued that smoothing the partial sum by integrating (averaging) over this period would remove the main effects of the ripple. This procedure is discussed next. The interested reader is referred to [Ham, $109$–$112$] for additional information.

The truncation, $\,T(f)$

Consider the truncation

$$ T(f) := \sum_{k=-K}^K C_k\,e^{i2\pi kf\Delta T} $$

of the infinite sum

$$ \text{Four}(\tilde H)(f) := \sum_{k=-\infty}^\infty C_k\,e^{i2\pi kf\Delta T} $$

The last terms kept correspond to indices $\,k = K\,$ and $\,k = -K\,,$ with corresponding period $\,\frac 1{K\Delta T}\,.$ Define a ‘smoothed’ function $\,S(f)\,,$ obtained by replacing the number $\,T(f)\,$ with the average value of the function $\,T\,$ over an interval of length $\,\frac 1{K\Delta T}\,$ centered at $\,f\,$:

$$ \begin{align} S(f) &:=\frac 1{1/(K\Delta T)}\int_{f-\frac 1{2K\Delta T}}^{f+\frac 1{2K\Delta T}} T(f)\,df\cr\cr &= \frac 1{1/(K\Delta T)}\int_{f-\frac 1{2K\Delta T}}^{f+\frac 1{2K\Delta T}} \sum_{k=-K}^K C_k\,e^{i2\pi kf\Delta T}\,df\cr\cr &= K\Delta T\sum_{k=-K}^K C_k \int_{f-\frac 1{2K\Delta T}}^{f+\frac 1{2K\Delta T}} e^{i2\pi kf\Delta T}\,df\cr\cr &= K\Delta T\sum_{k=-K}^K \frac{C_k}{\pi k\Delta T}\, e^{i2\pi kf\Delta T} \left[ \frac{ e^{i(\pi k/K)} - e^{-i(\pi k/K)}}{2i} \right]\cr\cr &= K\sum_{k=-K}^K \frac{C_k}{\pi k}\,e^{i2\pi kf\Delta T}\sin(\pi k/K)\cr\cr &= \sum_{k=-K}^K C_k \left[ \frac{\sin(\pi k/K)}{\pi k/K} \right]\, e^{i2\pi kf\Delta T} \end{align} $$
Sigma factors

Observe that in the resulting function $\,S(f)\,,$ the $\,k^{\text{th}}\,$ term of $\,T(f)\,$ has been scaled by the number:

$$ \frac{\sin(\pi k/K)}{\pi k/K} $$

These scaling factors are commonly called the sigma factors. Observe that:

$$ \begin{align} \frac{\sin\bigl( \pi(-k)/K\bigr)}{\pi(-k)/K} &= \frac{-\sin(\pi k/K)}{-\pi k/K}\cr\cr &= \frac{\sin(\pi k/K)}{\pi k/K} \end{align} $$

Also, when $\,k = 0\,,$ the sigma factor is defined to equal $\,1\,,$ since:

$$ \lim_{k\rightarrow 0} \frac{\sin(\pi k/K)}{\pi k/K} = 1 $$

The distinct values of the sigma factors are shown below, when $\,K = 10\,$:

$k$sigma factor
$0$$1$
$1$$0.9836$
$2$$0.9355$
$3$$0.8584$
$4$$0.7568$
$5$$0.6366$
$6$$0.5046$
$7$$0.3679$
$8$$0.2339$
$9$$ 0.1093$
$10$$0$
Example: Lanczos smoothing

The transfer functions of the previous example, after Lanczos smoothing is applied, become:

transfer function with Lanczos smoothing, K = 10 transfer function with Lanczos smoothing, K = 20

MATLAB IMPLEMENTATION: Finding a Symmetric Nonrecursive Filter Corresponding to a Desired Transfer Function

MATLAB function:   findfil

The MATLAB function  findfil , with source code given below, computes the coefficients of a symmetric nonrecursive filter corresponding to a desired transfer function.

To use the function, type:

[C,Hf,f] = findfil(tH,H,K,dT,smooth);

REQUIRED INPUTS

The required inputs are:

OPTIONAL INPUT
OUTPUTS

The function outputs three column vectors,  C ,  Hf , and  f .

Source code

The source code for the function  findfil  is given next: 

function [C,Hf,f] = findfil(tH,H,K,dT,smooth)
 if nargin==4
   smooth = 0;
 end
 N = length(tH);
 P = tH(N);
 C = zeros(K+1,1);
 C(1) = (1/N)*sum(H);
 for k = 2:(K+1)
   tvec = (2*pi*(k-1)*dT)*tH;
   cosv = cos(tvec);
   C(k) = (1/N)*sum(H .* cosv);
 end
 if smooth==1
   k = [1:K]';
     k = pi*k/K;
     sigma = sin(k) ./ k;
     C(2:K+1) = sigma .* C(2:K+1);
 end
 [Hf,f] = transfct(C,dT);
OCTAVE requires  endfunction  as the last line.
MATLAB function:   symtofc

The MATLAB function  symtofc  (‘symmetric to filter coefficients’) converts the $\,K+1\,$ distinct coefficients $\,c_0,c_1,\ldots,c_K\,$ from a nonrecursive symmetric filter, to the full set of coefficients

$$ c_{-K},\ldots,c_{-1},c_0,c_1,\ldots,c_K $$

(where $\,c_{-k} = c_k\,$), for use in the function  nonrec .

To use the function, type:

FC = symtofc(C); 

 function FC = symtofc(C);
 K = length(C) - 1;
 FC = flipud(C(2:(K+1)));
 FC = [FC;C];
OCTAVE requires  endfunction  as the last line.
INPUT and OUTPUT

The input is a column vector  C  containing the coefficients $\,c_0,c_1,\ldots,c_K\,.$

The output is a column vector  FC  containing the full set of coefficients $\,c_{-K},\ldots,c_{-1},c_0,c_1,\ldots,c_K\,.$

Example: Designing a low-pass filter

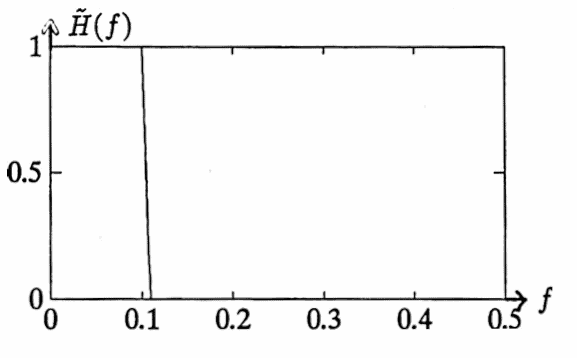
The following diary of an actual MATLAB session illustrates the use of the functions  findfil  and  symtofc . Here, a low-pass filter (which passes low frequencies, and suppresses high frequencies) is designed, corresponding to spacing $\,\Delta T = 1\,.$ The designed filter is then used to process a ‘known unknown’. 

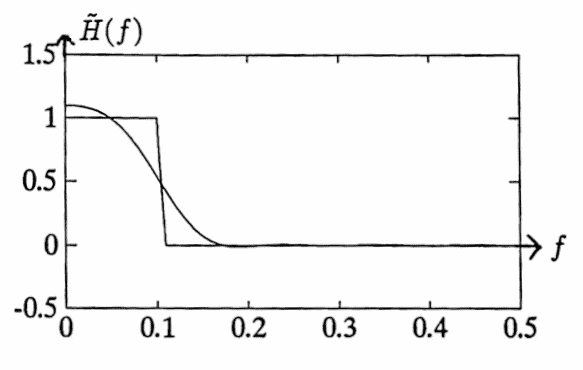
% Construct the desired transfer function:
 tH1 = [0:.01:.10]';
 tH2 = [.11:.01:.5]';
 y1 = ones(tH1);
 y2 = zeros(tH2);
 tH = [tH1;tH2];
 H = [y1;y2] ;
% Graph the desired transfer function:
 plot(tH,H)
Octave requires  ones(size(tH1))  and  zeros(size(tH2)) .
desired transfer function 
% Find a corresponding unsmoothed filter,
%   dT = 1, K = 10:
 [C,Hf,f] = findfil(tH,H,10,1);
% Plot the transfer function 
%   of the corresponding filter,
%   superimposed with the ideal transfer filter:
 plot(f,Hf)
 hold
Current plot held

 plot(tH,H)
 hold

Current plot released
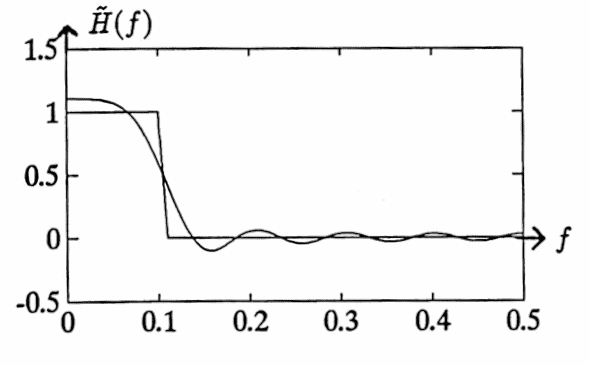
unsmoothed filter, dT = 1, K = 10 
% Now, find a corresponding smoothed filter,
%   dT = 1, K = 10:
 [C,Hf,f] = findfil(tH,H,10,1,1);
 plot(f,Hf)
 hold
     
Current plot held

 plot(tH,H)
 hold
 
Current plot released
smoothed filter, dT = 1, K = 10 
 C
% Here are the smoothed filter coefficients
%   c0,c1,...,c10 :
C =
     0.2157
     0.1978
     0.1506
     0.0905
     0.0359
     0.0000
    -0.0143
    -0.0129
    -0.0055
    -0.0002
     0.0000

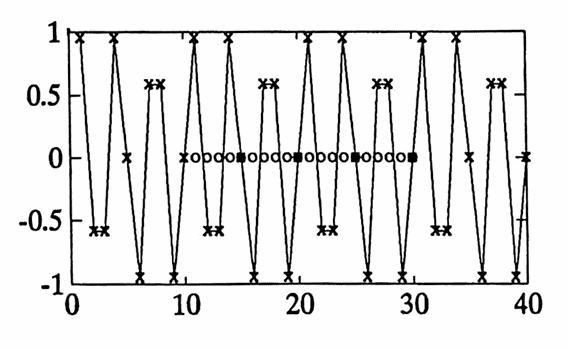
 t = [1:40]';
 y = sin(2*pi*.3*t)
 plot(t,y)
 hold
 
Current plot held

 plot(t,y,'x')
 FC = symtofc(C);
 D = [t y];
 [f,tf] = nonrec(D,FC);
 plot(tf,f,'o')
smoothed filter, dT = 1, K = 10