the Midpoint Formula

THE MIDPOINT FORMULA

The midpoint of the line segment between points $\,(x_1,y_1)\,$ and $\,(x_2,y_2)\,$ is given by the Midpoint Formula: $$ \left( \frac{x_1+x_2}2,\frac{y_1+y_2}2 \right) $$

Here, $\,x_1\,$ (read as ‘$\,x\,$ sub $\,1\,$’) denotes the $\,x$-value of the first point,
and $\,y_1\,$ (read as ‘$\,y\,$ sub $\,1\,$’) denotes the $\,y$-value of the first point.
Similarly, $\,x_2\,$ and $\,y_2\,$ denote the $\,x$-value and $\,y$-value of the second point.

Thus, to find the location that is exactly halfway between two points,
you average the x-values, and average the y-values.

The Midpoint Formula follows easily from the following observations:

The average of two numbers always lies exactly halfway between the two numbers.
Referring to the sketch below, $\Delta ABD\,$ is similar to $\,\Delta AMC$.
That is, these two triangles have the same angles.
Why? They both share angle $\,A\,$, and they both have a right angle.
Since all the angles in a triangle sum to $\,180^\circ\,$, the third angles must also be the same.
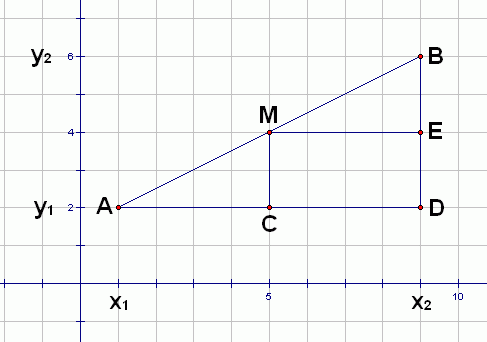
Similarity gives us what we need!
It tells us that $\Delta ABD\,$ and $\Delta AMC\,$ have exactly the same shapes—they're just different sizes.
Since $\,\overline{AM}\,$ is exactly half of $\,\overline{AB}\,$, $\,\overline{AC}\,$ must be exactly half of $\,\overline{AD}\,$.
Thus, $\,C\,$ is the midpoint between $\,A\,$ and $\,D\,$ (which can be found by averaging $\,x_1\,$ and $\,x_2\,$).
Use a similar argument to show that $\,\overline{DE}\,$ (which has the same length as $\,\overline{CM}\,$) is exactly half of $\,\overline{DB}\,$.

EXAMPLE:

Question:
Find the midpoint of the line segment between

$\,(1,-3)\,$ and $\,(-2,5)\,$.

Solution:

$\displaystyle \left( \frac{1+(-2)}2, \frac{-3 + 5}2 \right) = \left(-\frac12,1\right) $

Question:
Suppose that

$\,(2,3)\,$ is exactly halfway between $\,(-1,5)\,$ and $\,(x,y)\,$.
Find $\,x\,$ and $\,y\,$.

Solution:
Rephrasing, $\,(2,3)\,$ is the midpoint of the segment with endpoints $\,(-1,5)\,$ and $\,(x,y)\,$.
Thus:

$\displaystyle (2,3) = \left(\frac{-1+x}2,\frac{5+y}2\right) $	use the Midpoint Formula
$\displaystyle 2 = \frac{-1+x}2\ $ and $\ \displaystyle 3 = \frac{5+y}2$	for ordered pairs to be equal, the first coordinates must be equal and the second coordinates must be equal
$4 = -1 + x\ $ and $\ 6 = 5 + y$	clear fractions (multiply both sides of both equations by $\,2$)
$5 = x\ $ and $\ 1 = y$	finish solving each equation
$x = 5\ $ and $\ y = 1$	write your solutions in the conventional way

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
Introduction to Equations and Inequalities in Two Variables