Practice with the Distributive Law

One definition of the English verb to distribute is to spread out. The distributive law is one of the most frequently used tools in algebra, and tells how multiplication gets ‘spread out’ when it interacts with addition—it gives a different order of operations that can be used.

The basic statement of the distributive law is deceptively simple. Many important tools, however, are consequences of this law. One of the most famous is ‘FOIL’, which we'll see is a memory device for correctly multiplying expressions of the form $\,(a + b)(c + d)\,.$

The distributive law offers two different orders of operation that always give the same result:

• The expression $\,a(b + c)\,$ specifies this order: add $\,b\,$ to $\,c\,$;  then multiply $\,a\,$ by this sum.
• The expression $\,ab + ac\,$ specifies this order: multiply $\,a\,$ and $\,b\,$;  multiply $\,a\,$ and $\,c\,$;  then add these results.

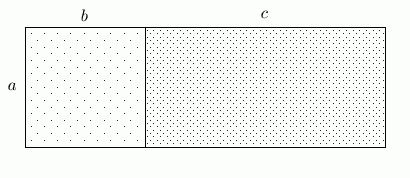
One effective visual way to understand the statement of the distributive law is to use areas (see below).

Form a rectangle with height $\,a\,$ and width $\,b + c\,.$ The area of this rectangle is height times width: $a(b + c)\,.$ However, the area can also be found by summing the areas of the two smaller rectangles: $\,ab + ac\,.$ Thus, $\,a(b + c) = ab + ac\,.$

It helps some students first learning to use the distributive law to draw the following arrows:

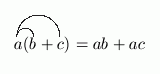
Examples

Practice