Verifying Trigonometric Identities

Thanks for your support!

 

Tools for Verifying Trigonometric Identities

Verifying identities is all about renaming—to show that two (initially different-looking) expressions are actually the same.
You'll use:

• familiar algebraic tools: e.g., factoring, distributive laws, getting common denominators
• definitions of the trigonometric functions $$ \cssId{s17}{\text{For simplicity, inputs are not shown:}}\qquad \cssId{s18}{\tan = \frac{\sin}{\cos}}\qquad \qquad \cssId{s19}{\cot = \frac{\cos}{\sin} = \frac{1}{\tan}}\qquad \qquad \cssId{s20}{\sec = \frac{1}{\cos}}\qquad \qquad \cssId{s21}{\csc = \frac{1}{\sin}} $$
• trigonometric identities that have already been proved
  This varies from teacher-to-teacher and course-to-course.
  Always ask about which identities you're allowed to use when verifying new ones.
  
  For the exercises in this section, you're only ‘allowed’ the three fundamental trigonometric identities cited above,
  together with two that follow immediately from the Pythagorean Identity:
  
  

  Start with:   $\,\sin^2 + \cos^2 = 1\,$ (For simplicity, inputs are not shown.)
  divide both sides by $\,\cos^2\,$: $$ \begin{gather} \cssId{s30}{\frac{\sin^2 + \cos^2}{\cos^2} = \frac{1}{\cos^2}}\cr\cr \cssId{s31}{\frac{\sin^2}{\cos^2} + \frac{\cos^2}{\cos^2} = \frac{1}{\cos^2}}\cr\cr \cssId{s32}{\left(\frac{\sin}{\cos}\right)^2 + 1 = \left(\frac{1}{\cos}\right)^2}\cr\cr\cr \cssId{s33}{\color{red}{\tan^2 + 1 = \sec^2}} \end{gather} $$	divide both sides by $\,\sin^2\,$: $$ \begin{gather} \cssId{s35}{\frac{\sin^2 + \cos^2}{\sin^2} = \frac{1}{\sin^2}}\cr\cr \cssId{s36}{\frac{\sin^2}{\sin^2} + \frac{\cos^2}{\sin^2} = \frac{1}{\sin^2}}\cr\cr \cssId{s37}{1 + \left(\frac{\cos}{\sin}\right)^2 = \left(\frac{1}{\sin}\right)^2}\cr\cr\cr \cssId{s38}{\color{red}{1 + \cot^2 = \csc^2}} \end{gather} $$

  
  In this lesson, the identities   ‘$\,\color{red}{\tan^2 x + 1 = \sec^2 x}\,$’   and   ‘$\,\color{red}{1 + \cot^2 x = \csc^2 x} \,$’
  are referred to as alternate Pythagorean Identities.
  
  You should be able to easily recognize equivalent versions of the five already-proved identities you're allowed to use in this section:
  the Pythagorean Identity and its two alternate versions, cosine is even, and sine is odd.
  
  For example, ‘$\,\sin^2 x = 1 - \cos^2 x\,$’ should be easily identified as an equivalent version of the Pythagorean Identity.
• Some Helpful Techniques:
  
  • Write Everything in Terms of Sines and Cosines:
    If an expression involves a ‘mix’ of trigonometric functions,
    it sometimes helps to write everything in terms of just sines and cosines.
  • the Conjugate Technique:
    By definition, $\,x + y\,$ and $\,x - y\,$ are called conjugates.
    Thus, the conjugate of $\,x + y\,$ is $\,x - y\,$; the conjugate of $\,x - y\,$ is $\,x + y\,.$
    
    When a numerator or denominator in a (suspected) trigonometric identity is of the form $\,1 \pm \sin x\,$ or $\,1\pm \cos x\,,$
    then it often helps to multiply both numerator and denominator by the conjugate.
    (Thus, you're multiplying the original expression by $\,1\,$ in the form $\,\frac{\text{conjugate}}{\text{conjugate}}\,.$ )
    
    Why? This reduces two terms to a single term, which is often easier to work with.
    Below are a couple examples. (Review FOIL as needed.) $$ \cssId{s57}{\overbrace{(1 - \sin x)}^{\text{original expression}}} \cssId{s58}{\cdot}\ \ \cssId{s59}{\overbrace{(1 + \sin x)}^{\text{conjugate}}} \qquad \cssId{s60}{\overbrace{=\strut}^{\text{FOIL}}}\qquad \cssId{s61}{1 - \sin^2 x} \cssId{s62}{\overbrace{=\strut}^{\text{Pythagorean Identity}}} \cssId{s63}{\cos^2 x} $$ $$ \cssId{s64}{\overbrace{(1 + \cos x)}^{\text{original expression}}} \cssId{s65}{\cdot}\ \ \cssId{s66}{\overbrace{(1 - \cos x)}^{\text{conjugate}}} \qquad \cssId{s67}{\overbrace{=\strut}^{\text{FOIL}}}\qquad \cssId{s68}{1 - \cos^2 x} \cssId{s69}{\overbrace{=\strut}^{\text{Pythagorean Identity}}} \cssId{s70}{\sin^2 x} $$ As illustrated in an example below, the conjugate technique often helps out for other binomial (two-term) expressions, too!
    

Two Basic Approaches for Verifying Identities

Equations of the form:
COMPLICATED = SIMPLER	COMPL1 = COMPL2
Often, one side of a (suspected) identity is more complicated than the other. In such cases, it is usually easiest to: start with the complicated side apply tools (one at a time) to rename it as the simpler side $$ \cssId{s79}{ \begin{align} \text{C O M}&\text{P L I C A T E D}\cr &= \ \text{<re-name>}\cr &= \ \text{<re-name>}\cr &= \ \ldots\cr &= \ \text{SIMPLER} \end{align}} $$	Often, both sides of a (suspected) identity are similarly complicated. In such cases, you can often work with each side separately, renaming each side as the same simpler expression: $$ \cssId{s83}{ \begin{align} \text{COMPL1} &= \ \text{<re-name>}\cr &= \ \ldots\cr &= \ \color{red}{\text{SIMPLER}}\cr\cr \text{COMPL2} &= \ \text{<re-name>}\cr &= \ \ldots\cr &= \ \color{red}{\text{SIMPLER}} \end{align}} $$ The two $\,\color{red}{\text{SIMPLER}}\,$ expressions are the same! (Sometimes, when renaming one side, you inadvertently end up with the other side. If so—you're done!)
Notes: if a complicated side is long, put the first simplication on the next line, indented a bit for readability, line up all equal signs you may want to provide a reason for each step MANY IDENTITIES CAN BE VERIFIED IN MANY DIFFERENT WAYS! (In the examples and exercises, only one correct approach is shown.)

EXAMPLE of ‘COMPLICATED = SIMPLER’:
Turning a Complicated Side into the Simpler Side

Verify the identity:     $\,\displaystyle \tan x + \frac{\cos x}{1 + \sin x} = \sec x\,$

SOLUTION:

The left side ($\,\tan x + \frac{\cos x}{1 + \sin x}\,$) is more complicated than the right side ($\,\sec x\,$).
Therefore, start with the expression on the left;
rename it to match the expression on the right.

The solution shown here first rewrites everything in terms of sines and cosines, and then uses the conjugate technique: $$ \begin{alignat}{2} &\cssId{s103}{\tan x + \frac{\cos x}{1 + \sin x}} &\qquad\qquad& \cssId{s104}{\text{(start with left side)}} \cr\cr &\qquad\cssId{s105}{= \ \frac{\sin x}{\cos x} + \frac{\cos x}{1 + \sin x}} &&\cssId{s106}{\text{(definition of tangent)}}\cr\cr &\qquad\cssId{s107}{= \ \frac{\sin x}{\cos x} + \frac{\cos x}{1 + \sin x}\cdot\frac{1 - \sin x}{1 - \sin x}} &&\cssId{s108}{\text{(conjugate technique)}}\cr\cr &\qquad\cssId{s109}{= \ \frac{\sin x}{\cos x} + \frac{(\cos x)(1 - \sin x)}{\cos^2 x}} &&\cssId{s110}{\text{(FOIL, Pythagorean Identity)}}\cr\cr &\qquad\cssId{s111}{= \ \frac{\sin x}{\cos x} + \frac{1 - \sin x}{\cos x}} &&\cssId{s112}{\text{(cancel)}}\cr\cr &\qquad\cssId{s113}{= \ \frac{1}{\cos x}} &&\cssId{s114}{\text{(add fractions)}}\cr\cr &\qquad\cssId{s115}{= \ \sec x} &&\cssId{s116}{\text{(definition of secant)}}\cr \end{alignat} $$

EXAMPLE of ‘COMPL1 = COMPL2’:
Working With Both Sides Separately

Verify the identity:     $\,\displaystyle \frac{1 + \cos t}{\cos t} = \frac{\tan^2 t}{\sec t - 1}\,$

SOLUTION:

The left side ($\,\frac{1 + \cos t}{\cos t}\,$) and the right side ($\,\frac{\tan^2 t}{\sec t - 1}\,$) are similarly complicated.
Therefore, work with both sides separately, trying to reduce each to the same simpler expression.
Here, ‘LHS’ and ‘RHS’ stand for ‘left-hand side’ and ‘right-hand side’.
Note that the conjugate technique is successfully applied to an expression of the form $\,\sec t - 1\,.$

$$ \begin{alignat}{2} &\cssId{s126}{\text{LHS}} \cssId{s127}{= \frac{1 + \cos t}{\cos t}} &\qquad\qquad& \cssId{s128}{\text{(start with LHS)}} \cr\cr &\qquad\cssId{s129}{= \ \frac{1}{\cos t} + \frac{\cos t}{\cos t}} &&\cssId{s130}{\text{(algebra)}}\cr\cr &\qquad\cssId{s131}{= \ \color{red}{\sec t + 1}} &&\cssId{s132}{\text{(definition of secant)}}\cr \end{alignat} $$

$$ \begin{alignat}{2} &\cssId{s133}{\text{RHS}} \cssId{s134}{= \frac{\tan^2 t}{\sec t - 1}} &\qquad\qquad& \cssId{s135}{\text{(start with RHS)}} \cr\cr &\qquad\cssId{s136}{= \ \frac{\tan^2 t}{\sec t - 1}\cdot\frac{\sec t + 1}{\sec t + 1}} &&\cssId{s137}{\text{(conjugate technique)}}\cr\cr &\qquad\cssId{s138}{= \ \frac{\tan^2 t(\sec t + 1)}{\sec^2 t - 1}} &&\cssId{s139}{\text{(FOIL)}}\cr\cr &\qquad\cssId{s140}{= \ \frac{\tan^2 t(\sec t + 1)}{\tan^2 t}} &&\cssId{s141}{\text{(alternate Pythagorean Identity)}}\cr\cr &\qquad\cssId{s142}{= \ \color{red}{\sec t + 1}} &&\cssId{s143}{\text{(cancel)}}\cr \end{alignat} $$

Notice that both the LHS and RHS have been renamed as the same expression, $\,\sec t + 1\,$.

Graphically Checking that an Equation is an Identity

For many years, I worked in a math lab. Any student could come in to get help.
I have a recollection of a time when I learned an important lesson.

I was helping someone verify an identity—but nothing was working! We tried oodles of things, for a very long time.
Finally, the thought occurred to me that perhaps it wasn't an identity after all—maybe it was just a mistake.
Indeed, it was a typo in the book.

If you ever find yourself in the same situation, check that you're really working with an identity.
If the LHS and RHS are always equal then they will have precisely the same graphs.

At WolframAlpha, if you type in two comma-separated expressions, then both will be graphed in the same coordinate system.
If you graph both sides of an identity, then it will look like a single graph, because the graphs will overlap perfectly!

For example, cut-and-paste the following into WolframAlpha:

tan(x) + cos(x)/(1 + sin(x)) , sec x
Here's what you'll see:

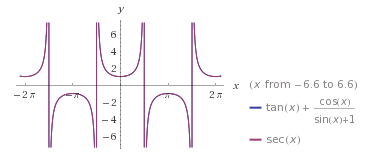
	The blue and red graphs overlap perfectly, giving the appearance of a single graph. This graphically shows that   ‘$\,\displaystyle \tan x + \frac{\cos x}{1 + \sin x} = \sec x\,$’   is an identity.
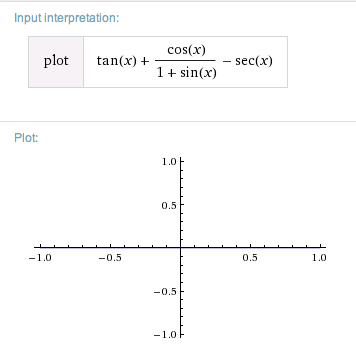	If you prefer, you can get an equivalent equation with zero on one side: $$\cssId{s163}{\tan x + \frac{\cos x}{1 + \sin x} - \sec x = 0}$$ Since this is an identity, the left side graphs as the zero function. Not much to see!

How to Prove that an Equation is NOT an Identity

If the graphs don't match up (and you've input both sides correctly), then you're not working with an identity.
To prove that a sentence is not an identity, you need only provide a single number for which the sentence is false.

For example, ‘$\,\displaystyle \tan x + \frac{\cos x}{1 + \sin x} = 1 + \sec x\,$’ is not an identity:

• when $\,x = 0\,,$ the LHS is:   $\displaystyle \,\tan 0 + \frac{\cos 0}{1 + \sin 0} = 0 + \frac{1}{1 + 0} = 1\,$
• when $\,x = 0\,,$ the RHS is:   $\displaystyle \,1 + \sec 0 = 1 + \frac{1}{\cos 0} = 1 + \frac{1}{1} = 2\,$
• $\,1\ne 2\,$

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
Addition and Subtraction Formulas for Sine and Cosine