 Testing Equations for Symmetry
Testing Equations for Symmetry
A knowledge of symmetry can increase your efficiency when working with graphs. This section discusses:
A graph has symmetry
about the $x$-axis
if and only if
whenever $\,(a,b)\,$ is on the graph,
so is $\,(a,-b)\,.$
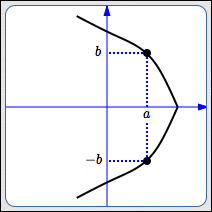
Here are some observations about graphs with $x$-axis symmetry:
- If you ‘fold’ the coordinate plane along the $x$-axis, the top and bottom portions of the graph overlap. That is, the $x$-axis acts as a ‘mirror’ for the graph.
- If $\,b \ne 0\,$ and $\,(a,b)\,$ is a point on the graph, then there must be a second, different, point on the graph, which has the same $x$-value but opposite $y$-value.
-
Most graphs with $x$-axis symmetry fail the vertical line test, and hence are not functions. (Recall that functions have the property that every input must have exactly one output.)
The zero function, $\,f(x) = 0\,,$ has $x$-axis symmetry, but is pretty boring!
- In-a-nutshell test for $x$-axis symmetry: Replace every $y$ by $-y\,,$ and see if the same equation results. (The example below gives more logical details.)
A graph has symmetry
about the $y$-axis
if and only if
whenever $\,(a,b)\,$ is on the graph,
so is $\,(-a,b)\,.$
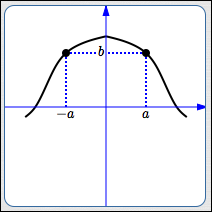
Here are some observations about graphs with $y$-axis symmetry:
- If you ‘fold’ the coordinate plane along the $y$-axis, the left and right portions of the graph overlap. That is, the $y$-axis acts as a ‘mirror’ for the graph.
- If $\,a \ne 0\,$ and $\,(a,b)\,$ is a point on the graph, then there must be a second, different, point on the graph, which has the same $y$-value but opposite $x$-value.
- In-a-nutshell test for $y$-axis symmetry: Replace every $x$ by $-x\,,$ and see if the same equation results. (The example below gives more logical details.)
A graph has symmetry
about the origin
if and only if
whenever $\,(a,b)\,$ is on the graph,
so is $\,(-a,-b)\,.$
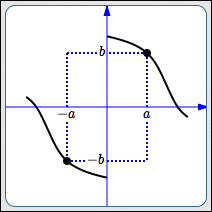
Here are some observations about graphs with origin symmetry:
- If you ‘fold’ the coordinate plane twice: once along the $x$-axis, and once along the $y$-axis; then the graph will overlap itself.
- If $\,(a,b)\,$ is a point on the graph where at least one of the coordinates is not zero, then there must be a second, different, point on the graph, which has opposite $x$ and $y$ values.
-
If a graph has both $x$-axis and $y$-axis symmetry, then it must have origin symmetry:
$$ \begin{align} &\cssId{s57}{(a,b)\text{ on graph}}\cr\cr &\qquad\cssId{s58}{\overset{\text{ $x$-axis sym }}{\Longrightarrow}} \cssId{s59}{(a,-b)\text{ on graph}}\cr\cr &\qquad\cssId{s60}{\overset{\text{ $y$-axis sym }}{\Longrightarrow}} \cssId{s61}{(-a,-b)\text{ on graph}} \end{align} $$ - In-a-nutshell test for origin symmetry: Replace every $x$ by $-x$ and every $y$ by $-y\,,$ and see if the same equation results. (The example below gives more logical details.)
Testing Equations in Two Variables For Symmetry
The following example illustrates the logic and procedure for testing an equation in two variables for symmetry about the $x$-axis, $y$-axis, and origin.
Example: Test $x^2y^3 - x^4y = y$ For Various Symmetries
Suppose $\,(a,b)\,$ is on the graph. Thus, substitution of ‘$\,a\,$’ for ‘$\,x\,$’ and ‘$\,b\,$’ for ‘$\,y\,$’ makes the equation true.
In other words, when every $x$-value is replaced by $\,a\,,$ and every $y$-value is replaced by $\,b\,,$ the resulting equation is true.
Thus, the following equation is assumed to be true:
$$ \cssId{s78}{a^2b^3 - a^4b = b} \tag{$\cssId{s79}{\dagger}$} $$This equation is given the name ‘$\,\dagger\,$’ (read as ‘dagger’) to make it easy to refer to in subsequent steps.
PROCEDURE
Test for Symmetry About the $x$-axis
- Does $\,(a,-b)\,$ also lie on the graph? That is, does substitution of ‘$\,a\,$’ for ‘$\,x\,$’ and ‘$\,-b\,$’ for ‘$\,y\,$’ yield a true equation?
- The question mark over the equal sign emphasizes that you're asking a question—is the equation true?
- Simplify the equation. If it is equivalent to $(\dagger)$ (which is assumed to be true), then it is true.
- If the equation is determined to be true, then drop the question mark over the equal sign.
EXAMPLE
$\color{blue}{x}^2\color{green}{y}^3 - \color{blue}{x}^4\color{green}{y} = \color{green}{y}$
$$\begin{gather} \cssId{s92}{\color{blue}{a}^2\color{green}{(-b)}^3 - \color{blue}{a}^4\color{green}{(-b)}\ \overset{?}{=}\ \color{green}{-b}} \cr\cr \cssId{s93}{-a^2b^3 + a^4b \ \overset{?}{=}\ -b}\cr\cr \cssId{s94}{a^2b^3 - a^4b = b}\cr \cssId{s95}{(\text{after multiplying both sides by $-1$})}\cr \cssId{s96}{\text{(True, by comparison with $\dagger$)}} \end{gather} $$The graph has $x$-axis symmetry, since whenever $\,(a,b)\,$ lies on the graph, so does $\,(a,-b)\,.$
Test for Symmetry About the $y$-axis
- Does $\,(-a,b)\,$ also lie on the graph? That is, does substitution of ‘$\,-a\,$’ for ‘$\,x\,$’ and ‘$\,b\,$’ for ‘$\,y\,$’ yield a true equation?
- The question mark over the equal sign emphasizes that you're asking a question—is the equation true?
- Simplify the equation. If it is equivalent to $(\dagger)$ (which is assumed to be true), then it is true.
- If the equation is determined to be true, then drop the question mark over the equal sign.
$x^2y^3 - x^4y = y$
$$\begin{gather} \cssId{s106}{(-a)^2b^3 - (-a)^4b\ \overset{?}{=}\ b} \cr\cr \cssId{s107}{a^2b^3 - a^4b = b}\cr \cssId{s108}{\text{(True, by comparison with $\dagger$)}} \end{gather} $$The graph has $y$-axis symmetry, since whenever $\,(a,b)\,$ lies on the graph, so does $\,(-a,b)\,.$
Test for Origin Symmetry
- Since the graph has $x$-axis and $y$-axis symmetry, it must also have origin symmetry. However, the test is shown here for completeness.
- Does $\,(-a,-b)\,$ also lie on the graph? That is, does substitution of ‘$\,-a\,$’ for ‘$\,x\,$’ and ‘$\,-b\,$’ for ‘$\,y\,$’ yield a true equation?
- The question mark over the equal sign emphasizes that you're asking a question—is the equation true?
- Simplify the equation. If it is equivalent to $(\dagger)$ (which is assumed to be true), then it is true.
- If the equation is determined to be true, then drop the question mark over the equal sign.
$x^2y^3 - x^4y = y$
$$\begin{gather} \cssId{s121}{(-a)^2(-b)^3 - (-a)^4(-b)\ \overset{?}{=}\ -b} \cr\cr \cssId{s122}{-a^2b^3 + a^4b \ \overset{?}{=}\ -b}\cr\cr \cssId{s123}{a^2b^3 - a^4b = b}\cr \cssId{s124}{(\text{after multiplying both sides by $-1$})}\cr \cssId{s125}{\text{(True, by comparison with $\dagger$)}} \end{gather} $$The graph has origin symmetry, since whenever $\,(a,b)\,$ lies on the graph, so does $\,(-a,-b)\,.$
By the way, the equation $x^2y^3 - x^4y = y$ is not easy to graph. However, WolframAlpha is up to the challenge!
Type in x^2y^3 - x^4y = y (cut-and-paste, if you want) and you'll see the following graph:
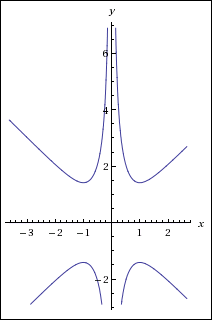
Look at the beautiful symmetries!
Or, use the WolframAlpha widget below! Click ‘Submit’ to see the picture of all points $\,(x,y)\,$ for which the equation is true. (Notice how the ‘^’ key is used to input powers.)
Play with other equations as you do the exercises below. Have fun!
Note: The exercise equations are randomly-generated for the purpose of giving you lots of practice testing equations for symmetry. Be prepared for some ‘strange’ results from WolframAlpha on some of the equations! Some equations may have only a single point that makes them true. Some equations may not have any real number solutions!