Two Useful Transforms: Reflection About the Line $\,y = x\,,$ and Counterclockwise Rotation by $90$ Degrees
This section is optional in the Precalculus course.
Once we have the ellipse equation for foci on the $x$-axis,
$$\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\,,$$we don't have to go through that long and tedious derivation a second time to get the equation for foci on the $y$-axis. There are easier ways!
If desired, we can use appropriate transforms to get the new graph. This section discusses two transforms that can be used.
Reflection About the Line $\,y = x$
As discussed in an earlier section, reflection about the line $\,y = x\,$ switches the coordinates of a point: $\,(x,y)\,$ moves to $\,(y,x)\,.$
For example, suppose that reflection about $\,y = x\,$ is applied to the ellipse $\,\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\,,$ which has its foci on the $x$-axis. Then:
- $\,(c,0)\,$ moves to $\,(0,c)$
- $\,(-c,0)\,$ moves to $\,(0,-c)$
So, the reflected ellipse has its foci on the $y$-axis.
In an equation, reflection about the line $\,y = x\,$ is accomplished by switching the variables $\,x\,$ and $\,y\,.$
For example, switching $\,x\,$ and $\,y\,$ turns
$$\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1$$into:
$$\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1$$As you'll see in the next section, this new equation is precisely the ellipse with center at the origin and foci along the $y$-axis! So easy!
Counterclockwise Rotation by $\,90^\circ$
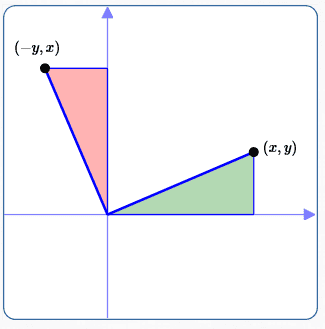
As illustrated by the sketch above, rotating counterclockwise by $\,90^\circ\,$ moves $\,(x,y)\,$ to $\,(-y,x)\,.$
Think of the green triangle as a wedge of wood; grab it and rotate it, so the side on the $x$-axis moves to the $y$-axis. It ‘turns into’ the red triangle!
How can an equation be ‘adjusted’ to accomplish this $\,90^\circ\,$ counterclockwise rotation?
Be very careful! Since $\,(x,y)\,$ moves to $\,(-y,x)\,,$ you might be tempted to think that, in the original equation, you should replace every $\,x\,$ by $\,-y\,$ and every $\,y\,$ by $\,x\,.$ But, this is wrong!
Here are the correct replacements in an equation, to rotate its graph counterclockwise by $\,90^\circ\,$:
- Replace every $\,x\,$ by $\,y$
- Replace every $\,y\,$ by $\,-x$
For example, applying a $\,90^\circ\,$ counterclockwise rotation to the equation $\,y = \sqrt{x}\,$ gives the following:
$$ \begin{gather} \overbrace{y}^{\text{replace by $\,-x\,$}} = \sqrt{\overbrace{x}^{\text{replace by $\,y\,$}}}\cr\cr -x = \sqrt{\vphantom{h}\, y\, } \end{gather} $$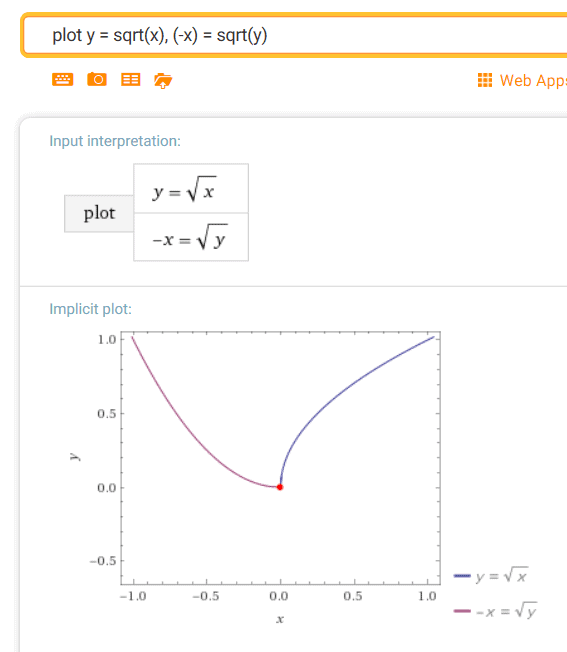
Look at the plot results above from WolframAlpha.
The equation $\,y = \sqrt x\,$ is plotted in blue.
The equation $\,-x = \sqrt y\,$ is plotted in purple.
Notice the beautiful $\,90^\circ\,$ counterclockwise rotation (from the blue curve to the purple curve), as desired!
So, What's Going On Here?
In a graph, we want $\,(x,y)\,$ to move to $\,(-y,x)\,.$ In the equation, this is accomplished by:
- Replacing every $\,x\,$ by $\,y$
- Replacing every $\,y\,$ by $\,-x$
Why does it work this way? What's going on here?
The Correct Thought Process
Here's the correct thought process:
Write the Equation in the Form $\,f(x,y) = 0$
Every equation in two variables ($\,x\,$ and $\,y\,$) can be written in the form $\,f(x,y) = 0\,.$ For example, the equation $\,y = x^2\,$ can be written as $\,y - x^2 = 0\,,$ so defining $\,f(x,y) := y - x^2\,$ does the job.
Graph of the Equation $\,f(x,y) = 0$
The graph of the original equation, $\,f(x,y) = 0\,,$ is (by definition):
$$ \{\ (x,y) \ \ |\ \ f(x,y) = 0\ \} \quad (*) $$Read ($*$) as: the set of all points $\,(x,y)\,$ with the property that $\,f(x,y) = 0\,.$
The Set of Points We Want
The set of points we want, after rotating the points in ($*$) counterclockwise by $\,90^\circ\,,$ is:
$$ \{\ (-y,x) \ \ |\ \ f(x,y) = 0\ \} \quad (**) $$Rewrite the Set of Points
Define $\,\hat x := -y\,$ and $\,\hat y := x\,,$ to view the points in ($**$) in a more natural way:
$$ \{\ (\ \overbrace{\strut -y}^{\hat x}\ ,\ \overbrace{\strut x}^{\hat y}\ ) \ \ |\ \ f(x,y) = 0\ \} \qquad (**) $$(Read $\,\hat x\,$ as ‘$x$ hat’ and $\,\hat y\,$ as ‘$y$ hat’.)
Solve for $\,x\,$ and $\,y\,$ in terms of $\,\hat x\,$ and $\,\hat y\,$:
$$ \begin{gather} x = \hat y\cr \text{and}\cr y = -\hat x \end{gather} $$Rename ($**$):
$$ \begin{align} &\{(\overbrace{\strut -y}^{\hat x},\overbrace{\strut x}^{\hat y}) \ \ |\ \ f(x,y) = 0\}\cr\cr &\quad = \{(\hat x,\hat y)\ \ |\ \ f(\hat y,-\hat x) = 0\}\cr\cr &\quad = \{(x,y)\ \ |\ \ f(y,-x) = 0\}\cr &\qquad\ \ \text{(return to the dummy}\cr &\qquad\ \ \text{variables $\,x\,$ and $\,y\,$)} \end{align} $$The Conclusion
How do we get from the original equation ‘$\,f(x,y) = 0\,$’ to the new (desired) equation ‘$\,f(y,-x) = 0\,$’ ? Answer: Replace every $\,x\,$ by $\,y\,,$ and replace every $\,y\,$ by $\,-x\,$!
I'm getting old, and need to safeguard my life's work.
After more than 25 years and 25,000 hours of developing this site, I am now seeking a successor organization to acquire OneMathematicalCat.org and carry it forward into the future. Learn more ➜
Want to say hello? Sign my guestbook!
Example
Rotate the ellipse $\displaystyle\,\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\,$ counterclockwise by $\,90^\circ\,$:
$$ \begin{gather} \frac{y^2}{a^2} +\frac{(-x)^2}{b^2} = 1\cr\cr \frac{y^2}{a^2} + \frac{x^2}{b^2} = 1 \end{gather} $$As before, you'll see in the next section that this is precisely the ellipse with center at the origin and foci along the $y$-axis!
Equations of Ellipses in Standard Form: Foci on the $y$-axis
Concept Practice
- Choose a specific problem type, or click ‘New problem’ for a random question.
- Think about your answer.
- Click ‘Check your answer’ to check!