Sketching Regions in the Coordinate Plane

You should be comfortable sketching simple regions in the coordinate plane, such as the examples below.

If things like ‘$\{\,(x,y)\ |\ x > 3\,\}$’ are uncomfortable for you, then be sure to read the discussion of set-builder notation further down on this page.

$x > 3$
Viewed as an inequality in two variables:
$x + 0y > 3$

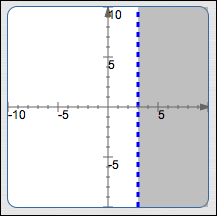
All points with $x$-value greater than $3\,$:
$\{\,(x,y)\ |\ x > 3\,\}$

$y \le 3$
Viewed as an inequality in two variables:
$0x + y \le 3$

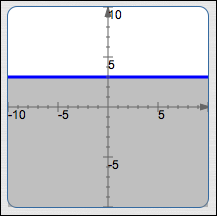
y <= 3, viewed as an inequality in two variables: 0x + y <= 3

All points with $y$-value less than or equal to $3\,$:
$\{\,(x,y)\ |\ y \le 3\,\}$

$xy \lt 0$
This is an inequality in two variables.

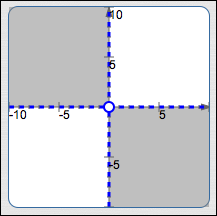
All points $(x,y)$ with $xy \lt 0\,$:
$\{\,(x,y)\ |\ xy \lt 0\,\}$

For the last example, note that:

$$ \begin{gather} \cssId{s19}{xy \lt 0}\cr \cssId{s20}{\text{is equivalent to}}\cr \cssId{s21}{(x \lt 0 \text{ and } y \gt 0)\ \ \text{ or }\ \ (x \gt 0 \text{ and } y \lt 0)} \end{gather} $$

That is, how can a product be negative? When exactly one of the factors is negative!

In the second quadrant, $\,x\,$ is negative and $\,y\,$ is positive.

In the fourth quadrant, $\,x\,$ is positive and $\,y\,$ is negative.

You can review the quadrants here. You can brush up on the mathematical words ‘and’, ‘or’, and ‘is equivalent to’ here . You can brush up on sentences in two variables here: Introduction to Equations and Inequalities in Two Variables. (Pay particular attention to the ‘invisible variable’ example near the bottom.)

I've copied some review of set-builder notation below. If you want a more thorough review of sets, study Advanced Set Concepts.

Set-Builder Notation

Often, it is convenient to describe a set by stating a property that members of the set must satisfy. In such cases, set-builder notation comes to the rescue.

Set-builder notation always has the following general form:

$$ \cssId{s37}{\{ x\ |\ \text{ a property that }\ x\ \text{ must satisfy } \}} $$

The vertical bar, ‘$\,|\,$’, is read as such that or with the property that.

For example:

$\{ x\ |\ x\gt 0\}$

can be read as

the set of all $\,x\,$ with the property that $\,x\,$ is greater than zero

Or:

$\{ x\ |\ x\gt 0\}$

can be read as

the set of all $\,x\,$ such that $\,x\,$ is greater than zero

Here's how those words attach themselves to different parts of the sentence:

$$ \cssId{s49}{\overset{\text{the set of all}}{\overbrace{\strut\ \ \{\ \ }}} \cssId{s50}{\overset{\text{ex}}{\overbrace{\strut\ \ x\ \ }}} \cssId{s51}{\underset{\text{with the property that}}{\underbrace{ \overset{\text{such that}}{\overbrace{\strut\ \ |\ \ }}}}} \cssId{s52}{\overset{\text{ex}}{\overbrace{\strut\ \ \ x\ \ }}} \cssId{s53}{\overset{\text{is greater than}}{\overbrace{\strut\ \ \gt\ \ }}}\ \ \cssId{s54}{\overset{\text{zero}}{\overbrace{\strut\ \ 0\ \ }}\ \ \}} $$

Notice that the closing brace, ‘$\,\}\,$’, is not verbalized. It is required, however, since it marks the end of the set structure.

Of course, sets often have different names. In the example above, the set could alternatively be described using interval notation:

$$ \cssId{s59}{\{ x\ |\ x\gt 0 \}} \cssId{s60}{= (0,\infty )} $$

Set-builder notation uses the concept of dummy variable. Roughly, a dummy variable is just a name given to something so that we have a way to talk about it; the name used doesn't affect the result.

Dummy variables are used in function notation:

‘$\,f(x)= x+2\,$’
describes the rule
‘take a number and add two’

Here, the dummy variable is $\,x\,.$

‘$\,f(t)=t+2\,$’
also describes the rule
‘take a number and add two’

Here, the dummy variable is $\,t\,.$

The set $\,\{x\ |\ x\gt 0\}\,$ can be written, using the dummy variable $\,t\,,$ as $\{t\ |\ t\gt 0\}\,.$ Or, it can be written, using the dummy variable $\,w\,,$ as $\,\{w\ |\ w\gt 0\}\,.$

Of course, it's a good idea to stick to the normal conventions for naming variables. For real numbers, use letters near the end of the alphabet. For integers, use letters near the middle of the alphabet.