Introduction to Trigonometry

Index card: 51ab

‘Trigonometry’ derives from the Greek, meaning literally ‘triangle measuring’. Because ‘trigonometry’ is such a long word, people often informally abbreviate it as ‘trig’.

The tools developed in trigonometry complement and expand those developed in geometry. For example, geometry's ‘ASA’ (angle-side-angle) congruence theorem states that a unique triangle is formed by two angles and the included side. But what are the lengths (measures) of those remaining two sides? Trigonometry gives the answer.

Trigonometry is used heavily in calculus (e.g., related rate problems and integration techniques), which is why it comprises a large part of any precalculus course.

Trigonometry is used in astronomy, navigation, architecture and land-surveying. The trigonometric functions are invaluable in studying any periodic (repetitive) phenomena. Love your cell phone and music CDs? Signal processing, noise cancellation, and music coding all use trigonometry.

Two Basic Approaches to Trigonometry: the Right Triangle and Unit Circle Approaches

There are two basic approaches to trigonometry:

the right triangle approach
the unit circle approach

These two approaches are ‘introduced via sketches’ below, and discussed thoroughly in the next two sections. You must know both approaches, because different problems favor one over the other.

Although at first glance the two approaches might seem totally different, they are actually beautifully intertwined: take one approach, apply a smidgeon of similar triangle theory, and the other pops out!

Goal of Both the Right Triangle and Unit Circle Approaches to Trigonometry

Both the ‘right triangle’ and ‘unit circle’ approaches have the same goal—to define the primary two trigonometric functions. These two functions are called sine and cosine:

formal (long) names:	sine	cosine
short names used in function notation:	sin	cos
pronunciations of both long and short names:	SINE (long i) (sounds like ‘sign’)	CO-sine (literally, ‘in company with the sine’)

Inputs and Outputs for Sine and Cosine

Recall that a function takes an input, and then uses this input to give a unique corresponding output.

For trigonometric functions, the input is the measure of an angle (for now), and the output is a real number.

Note for More Advanced Readers

Even though we're currently thinking of the trigonometric function input as the measure of an angle, later on we'll think of it as an arbitrary real number.

Important Convention

‘angle’ means ‘measure of the angle’

Strictly speaking, an angle is a geometric object. It is a set of points formed by the union of two rays that share a common endpoint. In trigonometry and beyond, however, it is the measure of the angle that is needed.

It's really inconvenient to always have to say ‘the measure of the angle’ instead of just ‘the angle’! So, from this point on in this web site curriculum, whenever we say ‘angle’ we really mean the measure of the angle!

For emphasis, let's repeat an earlier sentence with our new convention:

For trigonometric functions, the input is an angle (for now), and the output is a real number.

Outputs from Sine and Cosine are Extremely Simple!

As you'll see below, the outputs from sine and cosine are extremely simple!

In the right triangle approach, they're just ratios of lengths of sides of a triangle.

In the unit circle approach, they're just coordinates of a point.

Oh, that such incredible power and utility can come from such simple beginnings!

Information that is Common to Both the Right Triangle and Unit Circle Approaches

The following information is common to both approaches:

Start with attention focused on an angle.

In the right triangle approach, it's an angle in a triangle.

In the unit circle approach, it's an angle in a circle.
It is traditional to name the angle $\,\theta\,.$

‘$\,\theta\,$’ is the lowercase Greek letter ‘theta’ (pronounced THAY-ta).
Using $\,\theta\,$ as the input, the two primary trigonometric functions sine and cosine are defined. There are more trigonometric functions, but they're all defined in terms of sine and cosine.
It is conventional to drop the parentheses that typically hold the input when using function notation with the trigonometric functions. That is, when there is no ambiguity about order of operations:
- ‘$\sin(\theta)\,$’ is usually written as ‘$\sin\theta\,$’ (no parentheses), and is read aloud as ‘sine of theta’
- ‘$\cos(\theta)\,$’ is usually written as ‘$\cos\theta\,$’ (no parentheses), and is read aloud as ‘cosine of theta’

‘In a Nutshell’: the Right Triangle and Unit Circle Approaches

Here are ‘in a nutshell’ looks at the two approaches. For all the details, study the next two sections in this Precalculus course:

The Right Triangle Approach to Trigonometry

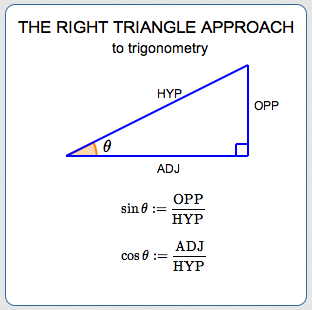
In the right triangle approach to trigonometry, the trigonometric functions are just ratios of lengths of sides in a right triangle!

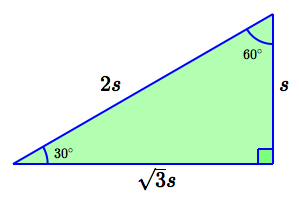
Here's an example, using the familiar $\,30^\circ$-$60^\circ$-$90^\circ\,$ triangle:

example of right triangle approach to trigonometry

$$ \begin{alignat}{2} \sin 30^\circ&\ \ =\ \ && \frac{s}{2s} &\ \ =\ \ && \frac 12\cr\cr \cos 30^\circ &\ \ =\ \ && \frac{\sqrt 3s}{2s} &\ \ =\ \ && \frac{\sqrt 3}2\cr\cr \sin 60^\circ &\ \ =\ \ && \frac{\sqrt 3s}{2s} &\ \ =\ \ && \frac{\sqrt 3}2\cr\cr \cos 60^\circ &\ \ =\ \ && \frac{s}{2s} &\ \ =\ \ && \frac 12 \end{alignat} $$

The Unit Circle Approach to Trigonometry

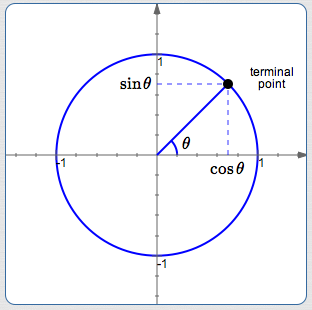
The circle above is centered at the origin and has radius equal to $\,1\,.$ It is called the ‘unit circle’.

In the unit circle approach to trigonometry, sine and cosine are just coordinates of a point on the unit circle!

The sketch below shows two ways to get to the same terminal point:

$30^\circ\,$
(positive angles are swept out counterclockwise; up)

$-330^\circ\,$
(negative angles are swept out clockwise; down)

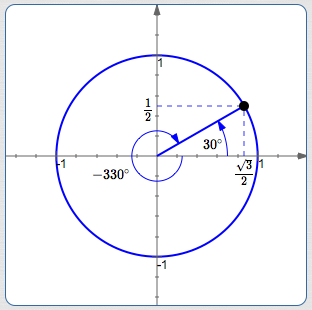
It doesn't matter how we get there! All that matters are the coordinates of the terminal point:

$$ \begin{gather} \cssId{s85}{\cos 30^\circ = \cos(-330^\circ) = \frac{\sqrt 3}{2}}\cr\cr \cssId{s86}{\sin 30^\circ = \sin(-330^\circ) = \frac{1}{2}} \end{gather} $$