Introduction to Instantaneous Rate of Change and Tangent Lines

The three curves (black, red, green) shown below illustrate three very different ways to travel from point $\,A\,$ to point $\,B\,.$

However, the average rate of change between $\,A\,$ and $\,B\,$ is precisely the same for all three curves. This is because average rate of change only uses information at the ends of the interval of interest—it is the slope of the line between the two points.

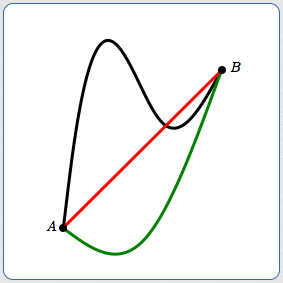
three different ways to travel from A to B

How, then, can we capture what is happening between $\,A\,$ and $\,B\,$? Instantaneous rate of change to the rescue!

Tangent Lines

Imagine walking along a curve, moving from left to right. At each point, the tangent line (when it exists) gives information about the ‘direction’ you're traveling at the instant you pass through that point.

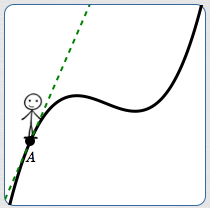
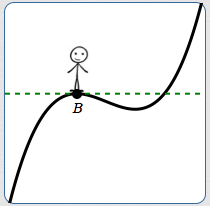
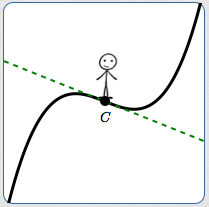
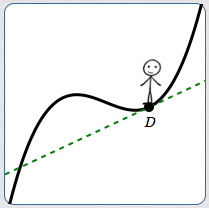
For example (above):

At $A$, you're rising quickly (going up a steep hill)
At $B$, you've leveled off (going horizontally)
At $C$, you're falling (going downhill)
At $D$, you're rising slowly (going up a gradual hill)

Tangent Lines Don't Always Exist

Tangent lines don't always exist. There are situations where there is no ‘direction you're traveling’ as you pass through a point. For example:

There is no tangent line at $\,E\,$ (below). There is a sudden change in direction (a ‘kink’) at $\,E\,.$ As you come up to $\,E\,$ you're traveling one direction, and as you leave you're traveling another direction.
There is no tangent line at $\,F\,$ (below). There is a ‘break’ at $\,F\,.$ You approach the ‘missing point’ along the curve, then you ‘jump’ to get to $\,F\,,$ and then ‘jump’ again to get back to the curve.

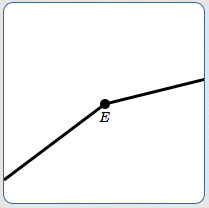
Tangent lines don't exist at kinks

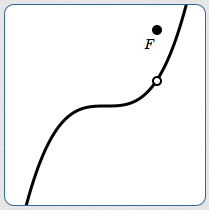
Tangent lines don't exist at breaks

Mathematics Cannot Rely on Intuition

Most people have very good intuition about how to draw tangent lines (when they exist). However, mathematics can't rely on intuition.

Here's the big problem with tangent lines: they typically touch the curve at the place of interest at only one point. Is one point enough to uniquely define a line? Absolutely not! Is one point enough to uniquely determine the slope of a line? Absolutely not!

Calculus solves these problems using the concept of limits.

Here's the idea, in a nutshell. Suppose we want to understand the tangent line to the black curve at point $\,P\,$ (below). The tangent line is shown in red.

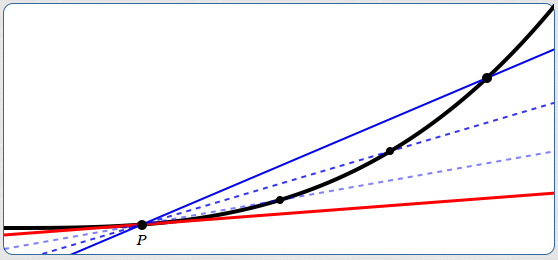
Choose a point on the curve that's ‘near’ $\,P\,$ and connect the dots, giving the solid blue line. This solid blue line is a (poor) approximation to the tangent line.
Slide the new point closer and closer to $\,P\,,$ giving the succession of lighter blue dashed lines. These give better and better approximations to the tangent line!
We can compute the slopes of all the approximating blue lines, since two points are known on each of these lines. These slopes are getting closer and closer to the slope of the tangent line.
The slope of the tangent line is called the instantaneous rate of change at $\,P\,.$

Instantaneous Rate of Change

The slope of a non-vertical tangent line (when it exists) is called instantaneous rate of change.

Instantaneous rate of change tells how fast outputs are changing, as compared to inputs, at the instant you pass through a point.

For example, suppose the slope of the tangent line at a point is $\,2\,.$ In other words, suppose the instantaneous rate of change at a point is $\,2\,.$ This means that at the instant you pass through the point, the outputs are changing twice as fast as the inputs. For example, if the inputs change by a small amount, we'd expect the outputs to change by about twice the amount.

But be careful! Slopes of tangent lines typically change as you move along a curve. In other words, instantaneous rate of change typically changes as you move along a curve. Remember—it's called instantaneous for a good reason. It's only guaranteed to hold for an instant—at a single point!