The Division Algorithm
The prior lesson introduced long division of polynomials.
Using long division, a ‘new name’ is obtained for a fraction of polynomials:
$$ \cssId{s3}{\frac{N(x)}{D(x)}} \cssId{s4}{= Q(x) + \frac{R(x)}{D(x)}}$$For example, long division renames
$$ \cssId{s6}{\frac{\overbrace{x^3-8x+2}^{N(x)}}{\underbrace{x+3}_{D(x)}}} $$as:
$$ \cssId{s8}{\overbrace{x^2 - 3x + 1}^{Q(x)} + \frac{\overbrace{\ \ -1\ \ }^{R(x)}}{\underbrace{\ x+3\ }_{D(x)}}} $$A quick-and-easy check gives some confidence that these two expressions are indeed the same:
The new expression for the fraction that is obtained by long division is often better to work with than the original.
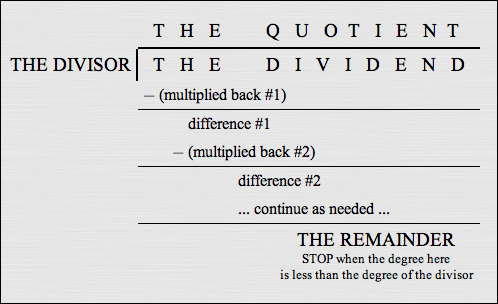
Terminology Used in the Long Division Process
In the long division process, when $\displaystyle\,\frac{\color{green}{N(x)}}{\color{red}{D(x)}}\,$ is renamed as $\displaystyle\,\color{blue}{Q(x)} + \frac{\color{orange}{R(x)}}{\color{red}{D(x)}}\,$:
- $\color{green}{N(x)}\,$ is often called the dividend (it's the numerator of the original fraction)
- $\color{red}{D(x)}\,$ is called the divisor (it's what you're dividing by; it's the denominator of the original fraction)
- $\color{blue}{Q(x)}\,$ is called the quotient
- $\color{orange}{R(x)}\,$ is called the remainder
The Division Algorithm (below) firms up details about division of polynomials. Here, the notation ‘$\,\text{deg}(P(x))\,$’ is used to denote the degree of a polynomial $\,P(x)\,.$
Let $\,N(x)\,$ and $\,D(x)\,$ be polynomials, with $\,D(x)\ne 0\,.$
There exist unique polynomials $\,Q(x)\,$ (called the quotient) and $\,R(x)\,$ (called the remainder) such that
$$ \cssId{s39}{\frac{N(x)}{D(x)} = Q(x) + \frac{R(x)}{D(x)}} $$or, equivalently,
$$ \cssId{s41}{N(x) = D(x)Q(x) + R(x)} $$where either
- $R(x) = 0\,$; or
- $\deg(R(x)) \lt \text{deg}(D(x))$
Notes About the Division Algorithm
What Does $\,Q(x)\,$ Tell You?
Think of $\,Q(x)\,$ as answering the question:
How many times does $\,D(x)\,$ go into $\,N(x)\,$?
What Does $\,R(x)\,$ Tell You?
Think of $\,R(x)\,$ as answering the question:
How much is left over?
When is the Long Division Procedure Stopped?
As shown in Long Division of Polynomials, the long division process is stopped when the degree of the expression you get after subtracting is less than the degree of the divisor.
This is the condition ‘$\,\text{deg}(R(x)) \lt \text{deg}(D(x))\,$’.
What Does $\,R(x) = 0\,$ Mean?
If the remainder is zero, then the divisor and quotient are both factors of the numerator—each goes in evenly.
To see this, substitute $\,R(x) = 0\,$ into
$$\frac{N(x)}{D(x)} = Q(x) + \frac{R(x)}{D(x)}$$to get:
$$\frac{N(x)}{D(x)} = Q(x)$$Multiplying through by $\,D(x)\,$ gives the equivalent equation
$$N(x) = D(x)Q(x)$$which shows that $\,D(x)\,$ and $\,Q(x)\,$ are both factors of $\,N(x)\,.$
As an example, study the two long division problems below, both of which result in remainders of zero:
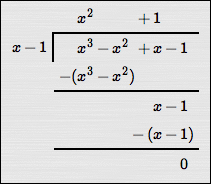$$\cssId{s67}{\frac{x^3 - x^2 + x - 1}{x-1} = x^2 + 1}$$
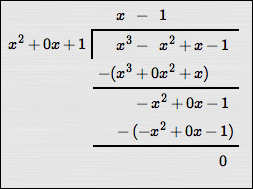$$\cssId{s68}{\frac{x^3 - x^2 + x - 1}{x^2+1} = x - 1}$$
Or, equivalently:
$$\cssId{s70}{x^3 - x^2 + x - 1 = (x-1)(x^2 + 1)}$$What Happens if the Degree of $\,N(x)\,$ is Less Than the Degree of $\,D(x)\,$ in the Expression $\,\frac{N(x)}{D(x)}\,$?
In this case, there is nothing to do! The quotient is zero, and the remainder is $\,N(x)\,.$
For example:
$$ \cssId{s76}{\frac{\overbrace{x + 1}^{\text{deg}(N(x)) = 1}}{\underbrace{x^2-3}_{\text{deg}(D(x)) = 2}}} \cssId{s77}{= \overbrace{\ \ 0\ \ }^{Q(x)} + \frac{\overbrace{x + 1}^{R(x)=N(x)}}{x^2 - 3}} $$The interesting application of the division algorithm is when the degree of $\,N(x)\,$ is greater than (or equal to) the degree of $\,D(x)\,.$ In this case, the long division process can be used to find the quotient and remainder.
I've Heard About ‘Synthetic Division’. What is it?
Synthetic division is an efficient shortcut for a special type of division problem—when the divisor is of the form $\,x + c\,.$
For example, $\,\frac{\text{a polynomial}}{x + 2}\,$ or $\,\frac{\text{a polynomial}}{x - 2}\,$ could be done using synthetic division.
However, $\,\frac{\text{a polynomial}}{3x + 2}\,$ can't be done using synthetic division, since the coefficient of the $\,x\,$ term must be one.
Also, $\,\frac{\text{a polynomial}}{x^2 + 3}\,$ can't be done using synthetic division, since the variable is only allowed to be raised to the first power.
Synthetic division is covered in the next section.