Long Division of Polynomials

This section has randomly-generated step-by-step long division practice for polynomials. Practice to your heart's content!

In this section, hovering over any yellow-highlighted item will highlight a related term in the long division process. Moving away will ‘release’ the highlighting. This should make it easier for you to connect written instructions to corresponding actions in the division problems.

(Try it by hovering here and then moving away!)

Long Division of Numbers

Think back to the long division of your grammar school days, say $\,1839\,$ divided by $\,7\,$:

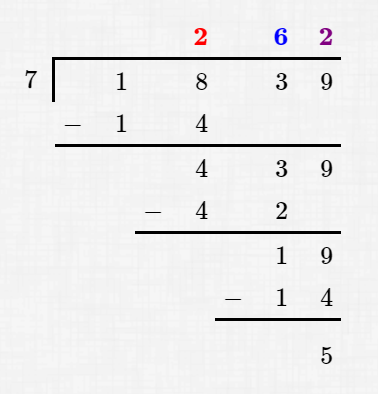
Recall your thought process:

				$\color{red}{\bf{2}}$
$7$		$1$		$8$		$3$	$9$

$7$ doesn't go into $1$

It goes into $18$ two times.

			$\color{red}{\bf{2}}$
$7$		$1$	$8$	$3$	$9$
	$-$	$1$	$4$

$2$ times $7$ is $14$

Subtract from previous row.

			$\color{red}{\bf{2}}$	$\color{blue}{\bf{6}}$
$7$		$1$	$8$	$3$	$9$
	$-$	$1$	$4$
			$4$	$3$	$9$

$8 - 4 = 4$

Bring down remaining digits.

$7$ goes into $43$ six times

				$\color{red}{\bf{2}}$	$\color{blue}{\bf{6}}$
$7$		$1$		$8$	$3$	$9$
	$-$	$1$		$4$
				$4$	$3$	$9$
			$-$	$4$	$2$

$6$ times $7$ is $42$

Subtract from previous row.

				$\color{red}{\bf{2}}$	$\color{blue}{\bf{6}}$	$\color{purple}{\bf{2}}$
$7$		$1$		$8$	$3$	$9$
	$-$	$1$		$4$
				$4$	$3$	$9$
			$-$	$4$	$2$
					$1$	$9$

$3 - 2 = 1$

Bring down remaining digit.

$7$ goes into $19$ two times

				$\color{red}{\bf{2}}$		$\color{blue}{\bf{6}}$	$\color{purple}{\bf{2}}$
$7$		$1$		$8$		$3$	$9$
	$-$	$1$		$4$
				$4$		$3$	$9$
			$-$	$4$		$2$
						$1$	$9$
					$-$	$1$	$4$

$2$ times $7$ is $14$

Subtract from previous row.

				$\color{red}{\bf{2}}$		$\color{blue}{\bf{6}}$	$\color{purple}{\bf{2}}$
$7$		$1$		$8$		$3$	$9$
	$-$	$1$		$4$
				$4$		$3$	$9$
			$-$	$4$		$2$
						$1$	$9$
					$-$	$1$	$4$
							$5$

$9 - 4 = 5$ is less than the divisor (which is $7$), so stop the process and summarize results.

				$\color{red}{\bf{2}}$		$\color{blue}{\bf{6}}$	$\color{purple}{\bf{2}}$
$7$		$1$		$8$		$3$	$9$
	$-$	$1$		$4$
				$4$		$3$	$9$
			$-$	$4$		$2$
						$1$	$9$
					$-$	$1$	$4$
							$5$

How many times does $\,7\,$ go into $\,1839\,$?
$\,262\,$ times

How much is left over? $\,5\,$

Notice that we stopped the process with the difference of $\,5\,.$

Thus, we never let $\,7\,$ ‘go into’ $\,5\,.$ So, $\,5\,$ still needs to be divided by $\,7\,$ !

So, here is one way to summarize the division problem:

$$\cssId{s25}{\frac{1839}{7} = 262 + \frac{5}{7}}\qquad\qquad \cssId{s26}{(\dagger)}$$

Note: the symbol ‘$\dagger$’ is read as ‘dagger’. You will often see this dagger symbol used to label important information.

Equation $(\dagger)$ often appears in a different form, as shown below:

$$\cssId{s31}{\frac{1839}{7} = 262 + \frac{5}{7}}$$

Start with equation $(\dagger)\,.$

$$\cssId{s33}{7\left( \frac{1839}{7} \right) = 7(262) + 7(\frac 57)}$$

Multiply both sides by $\,7\,.$

				$\color{red}{\bf{2}}$		$\color{blue}{\bf{6}}$	$\color{purple}{\bf{2}}$
$7$		$1$		$8$		$3$	$9$
	$-$	$1$		$4$
				$4$		$3$	$9$
			$-$	$4$		$2$
						$1$	$9$
					$-$	$1$	$4$
							$5$

$\,1839\,$ $=$ $\,7\,$ $\cdot$ $\,262\,$ $+$ $\,5\,$

Cancel extra factors of $\,1\,.$

This is an equivalent way to summarize the division problem.

Long Division of Polynomials

The long division of polynomials process is similar, with just a few extra considerations.

To illustrate, consider this division problem:

$$\cssId{s41}{\frac{x^3 - 8x + 2}{x+3}}$$

We want to know:

How many times does $\ x+3\ $ go into $\,x^3 - 8x + 2\,$ ?
How much is left over?

To begin:

Make sure that both the numerator and denominator are written in standard form, with the highest power first and then descending powers.
Put in zero terms for any missing powers.
For example, write $\ x^3 - 8x + 2\ $ as: $$x^3 \color{red}{+ 0x^2} - 8x + 2$$
For the ‘goes into’ process, ignore the $\,\color{red}{3}\,$ in $\,x+\color{red}{3}\,.$ That is, just say:

How many times does $\ x\ $ go into ... ?
In ‘the thought process’ below, hover over each highlighted term to locate the corresponding term in the division problem.

The Thought Process

$\color{red}{x^2}$

$x$

$+ \ 3\ $

$x^3$

$+$

$0x^2$

$-$

$8x$

$+$

$2$

$x$ goes into $\,x^3\,$ how many times?

$\displaystyle\frac{x^3}{x} = $ $\color{red}{x^2}$

$\color{red}{x^2}$

$x$

$+ \ 3\ $

$x^3$

$+$

$0x^2$

$-$

$8x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$x^3$

$+$

$3x^2$

$\color{green}{\bf{)}}$

$x^2$ $(x+3)$ $=$ $x^3 + 3x^2\ $

Subtract from previous row (put parentheses and minus sign).

$\color{red}{x^2}$

$\color{blue}{-\quad 3x}$

$x$

$+ \ 3\ $

$x^3$

$+$

$0x^2$

$-$

$8x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$x^3$

$+$

$3x^2$

$\color{green}{\bf{)}}$

$-3x^2$

$-$

$8x$

$+$

$2$

$0x^2 - 3x^2 = -3x^2$

Bring down remaining terms.

$x$ goes into $\,-3x^2\,$ how many times?

$\displaystyle\frac{-3x^2}{x} = $ $\color{blue}{-3x}$

$\color{red}{x^2}$

$\color{blue}{-\quad 3x}$

$x$

$+ \ 3\ $

$x^3$

$+$

$0x^2$

$-$

$8x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$x^3$

$+$

$3x^2$

$\color{green}{\bf{)}}$

$-3x^2$

$-$

$8x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$-3x^2$

$-$

$9x$

$\color{green}{\bf{)}}$

$-3x(x+3) = -3x^2 - 9x$

Subtract from previous row (put parentheses and minus sign).

$\color{red}{x^2}$

$\color{blue}{-\quad 3x}$

$\color{purple}{+\quad 1}$

$x$

$+ \ 3\ $

$x^3$

$+$

$0x^2$

$-$

$8x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$x^3$

$+$

$3x^2$

$\color{green}{\bf{)}}$

$-3x^2$

$-$

$8x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$-3x^2$

$-$

$9x$

$\color{green}{\bf{)}}$

$x$

$+$

$2$

$-8x - (-9x) = x$

Bring down remaining term.

$x\,$ goes into $x\,$ how many times?

$\displaystyle\frac{x}{x} = $ $\color{purple}{1}$

$\color{red}{x^2}$

$\color{blue}{-\quad 3x}$

$\color{purple}{+\quad 1}$

$x$

$+ \ 3\ $

$x^3$

$+$

$0x^2$

$-$

$8x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$x^3$

$+$

$3x^2$

$\color{green}{\bf{)}}$

$-3x^2$

$-$

$8x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$-3x^2$

$-$

$9x$

$\color{green}{\bf{)}}$

$x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$x$

$+$

$3$

$\color{green}{\bf{)}}$

$1(x+3) = x + 3$

Subtract from previous row (put parentheses and minus sign).

$\color{red}{x^2}$

$\color{blue}{-\quad 3x}$

$\color{purple}{+\quad 1}$

$x$

$+ \ 3\ $

$x^3$

$+$

$0x^2$

$-$

$8x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$x^3$

$+$

$3x^2$

$\color{green}{\bf{)}}$

$-3x^2$

$-$

$8x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$-3x^2$

$-$

$9x$

$\color{green}{\bf{)}}$

$x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$x$

$+$

$3$

$\color{green}{\bf{)}}$

$-1$

$2 - 3 = -1$

The degree of $\,-1\,$ is less than the degree of $\,x+3\,$, so stop the process and summarize results.

$\color{red}{x^2}$

$\color{blue}{-\quad 3x}$

$\color{purple}{+\quad 1}$

$x$

$+ \ 3\ $

$x^3$

$+$

$0x^2$

$-$

$8x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$x^3$

$+$

$3x^2$

$\color{green}{\bf{)}}$

$-3x^2$

$-$

$8x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$-3x^2$

$-$

$9x$

$\color{green}{\bf{)}}$

$x$

$+$

$2$

$\color{green}{\bf{-}}$

$\color{green}{\bf{(}}$

$x$

$+$

$3$

$\color{green}{\bf{)}}$

$-1$

How many times does $\,x+3\,$ go into $\,x^3 - 8x + 2\,$?

$\,x^2 - 3x + 1\,$ times

How much is left over? $\,-1\,$

Thus:

$$\cssId{s67}{\frac{x^3 - 8x + 2}{x+3} = x^2 - 3x + 1 + \frac{(-1)}{x+3}}$$

Or, equivalently:

$\,x^3 - 8x + 2\,$ $=$ $\,(x+3)\,$ $\,(x^2 - 3x + 1)\,$ $+$ $\,(-1)$

(True statements resulting from substituting particular values into the sentence that summarizes the long division)

Substitute this number ...

... into the sentence $$x^3 - 8x + 2 = (x+3)(x^2-3x+1) + (-1)$$

Comment:

$x = 0$

$$ \begin{gather} 0^3 - 8\cdot 0 + 2 \ \overset{?}{=}\ (0+3)(0^2 - 3\cdot 0 + 1) + (-1)\cr\cr 2 \ \overset{?}{=}\ 3(1) + (-1)\cr\cr 2 = 2 \end{gather} $$

It's easy to evaluate the expressions when $\,x\,$ is zero. This is an excellent quick check to gain some confidence that you did the long division correctly.

$x = 1$

$$ \begin{gather} 1^3 - 8\cdot 1 + 2 \ \overset{?}{=} \ (1+3)(1^2 - 3\cdot 1 + 1) + (-1)\cr\cr 1 - 8 + 2 \ \overset{?}{=}\ 4(1 - 3 + 1) + (-1)\cr\cr -5 = -5 \end{gather} $$

It's also quite easy to evaluate the expressions when $\,x\,$ is $\,1\,.$

It's nice to put a question mark over the equal sign until you're sure that the equation is true! Otherwise, you might be left looking at something like ‘$\,2 = 3\,$’, which can be uncomfortable—and tells you that you made a mistake in the long division process!

$x = -1$

$$ \begin{gather} (-1)^3 - 8(-1) + 2\cr \overset{?}{=}\cr (-1+3)\bigl((-1)^2 - 3(-1) + 1) + (-1)\bigr)\cr\cr -1 + 8 + 2 \ \overset{?}{=}\ 2(1 + 3 + 1) + (-1)\cr\cr 9 = 9 \end{gather} $$

It's also quite easy to evaluate the expressions when $\,x\,$ is $\,-1\,.$

Or, check for all values of $\,x\,$!

$$ \begin{align} &(x+3)(x^2 - 3x + 1) + (-1)\cr &\quad = x(x^2 - 3x + 1) + 3(x^2 - 3x + 1) - 1\cr &\quad = x^3 - 3x^2 + x + 3x^2 - 9x + 3 - 1\cr &\quad = x^3 - 8x + 2 \end{align} $$ OR $$ \begin{align} &(x+3)(x^2 - 3x + 1) + (-1)\cr &\quad = (x+3)(x^2) - (x+3)(3x) + (x+3)(1) - 1\cr &\quad = x^3 + 3x^2 - 3x^2 - 9x + x + 3 - 1\cr &\quad = x^3 - 8x + 2 \end{align} $$

In a linear algebra class, you'll learn that if you have $\,n\,$ non-overlapping, non-contradictory equations in $\,n\,$ unknowns, then this uniquely determines the $\,n\,$ unknowns.

A degree $\,n\,$ polynomial is determined by $\,n+1\,$ unknowns (the $\,n\,$ coefficients and the constant term).

Thus, $\,n+1\,$ points uniquely determine a polynomial of degree $\,n\,.$

So, if two cubic polynomials agree at four points, then they must agree everywhere. But, there's an easier check—just use the distributive law to multiply out the right-hand side, and combine like terms!

Using Web-Based Technology for Long Division of Polynomials

Of course, WolframAlpha can do division of polynomials!

The widget below computes: $$\frac{\text{numerator}}{\text{denominator}}$$

Type in any numerator and denominator that you want, and then press ‘Submit’. Have fun!

Step-by-Step Long Division Practice

Press the ‘Click here for a new Long Division Problem’ button (below) to begin.

Then, press the ‘Click here to Show Each Step’ button to cycle through all the steps in the long division process.

Enjoy!

Click here for a new

(The long division problem will appear here.)

Think about each step. Then:

Click here to

(Comments will appear here.)

(All the steps to the division problem will appear here.)

Long Division of Polynomials

Long Division of Numbers

Long Division of Polynomials

The Thought Process

Using Web-Based Technology for Long Division of Polynomials

Step-by-Step Long Division Practice

Concept Practice