Intersecting an Infinite Double Cone and a Plane: Looking at the Equations
This section is optional in the Precalculus course. There are no exercises in this section.
This section addresses a question about conics which may have arisen as you studied Identifying Conics by the Discriminant.
The question is: How do we know that intersections of an infinite double cone and a plane give rise to an equation of the form shown here?
$$Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0\quad \text{(*)}$$The purpose of this section is not to give a complete answer to this question. Instead, the purpose is to give enough information—at a level within the grasp of an ambitious Precalculus student—to make the answer plausible.
How Do We Know that Intersections of an Infinite Double Cone and a Plane Give Rise to an Equation of the Form Given in (*)?
We'll proceed as follows:
- Derive the equation of an infinite double cone (with known side steepness) in an $xyz$-coordinate system.
- Talk about the equation of a plane in an $xyz$-coordinate system.
- Algebraically find the intersection of the cone and the plane by solving the two equations simultaneously.
- Observe that the intersection is an equation with terms of type $\,x^2\,,$ $\,xy\,,$ $\,y^2\,,$ $\,x\,,$ $\,y\,,$ and constants.
Derive the Equation of an Infinite Double Cone
Three-Dimensional Coordinate System
Use this $xyz$-coordinate system:
- positive $\,x\,$ to the right
- positive $\,z\,$ straight up
- positive $\,y\,$ straight in
What We Seek
We seek an equation involving $\,x\,,$ $\,y\,$ and $\,z\,$ that is true for every point on an infinite double cone.
Equation of Line to be Rotated
Get the equation of the line that will be rotated about the $z$-axis to generate the cone:
In the $xz$-plane (not the $xy$-plane!) draw a line of slope $\,m\,$ through the origin (as shown below). It has equation $\,z = mx\,.$ (This is the familiar ‘$\,y = mx\,$’ with $\,z\,$ replacing $\,y\,.$)
A typical point (call it $\,P\,$) on this line has coordinates $\,(\frac zm,z)\,.$ (Why? Solve $\,z = mx\,$ for $\,x\,$ to get $\, x = \frac zm\,.$)
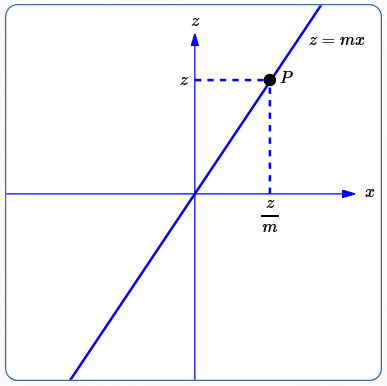
(The positive $\,y\,$ axis goes into the page)
Rotate Line
Rotate this line about the $z$-axis to create an infinite double cone. When rotated, point $\,P\,$ creates a circle of radius $\,\frac{z}{m}\,$ in a a plane parallel to the $xy$-plane.
Equation of Circle
Recall: the equation of a circle with radius $\,r\,$ through the origin is: $\,x^2 + y^2 = r^2\,.$ Thus, the circle that $\,P\,$ creates has equation:
$$ \begin{gather} x^2 + y^2 = \left(\frac{z}{m}\right)^2\cr\cr x^2 + y^2 = \frac{z^2}{m^2}\cr\cr m^2x^2 + m^2y^2 = z^2\cr\cr (mx)^2 + (my)^2 = z^2 \qquad (\,\dagger\,) \end{gather} $$Equation of an Infinite Double Cone
Equation ($\,\dagger\,$) is the equation of an infinite double cone with side steepness $\,m\,.$
Below are some WolframAlpha plots of infinite double cones. The second and third plots look the same, but the scales are different—look carefully!
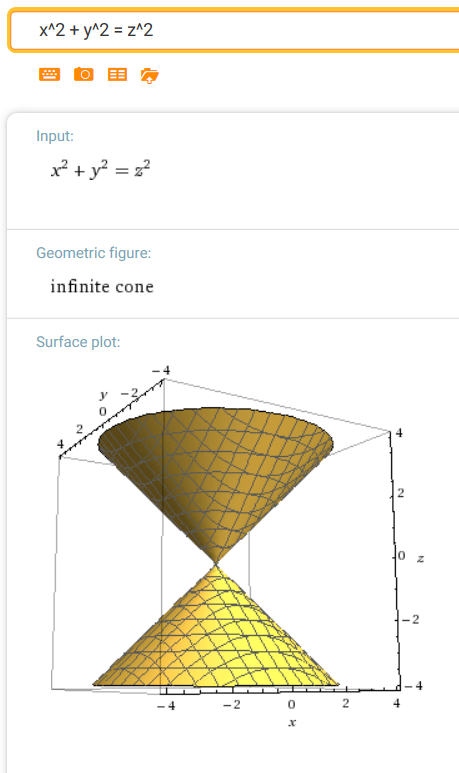
$x^2 + y^2 = z^2$
($\,m = 1\,$)
Observe that when $\,x = 4\,$ and $\,y = 0\,,$
$\,z\,$ is $\,1\cdot 4 = 4\,.$
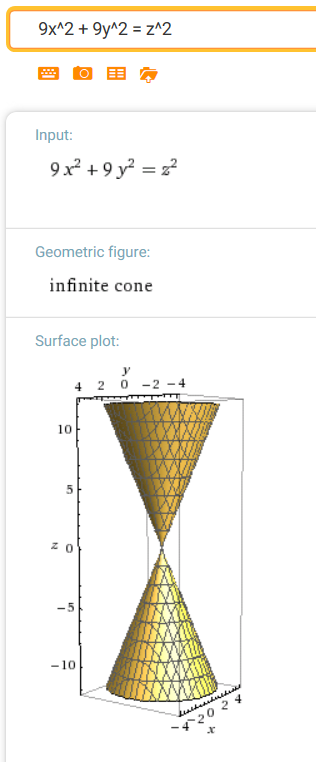
$(3x)^2 + (3y)^2 = z^2$
($\,m = 3\,$)
Observe that when $\,x = 4\,$ and $\,y = 0\,,$
$\,z\,$ is $\,3\cdot 4 = 12\,.$
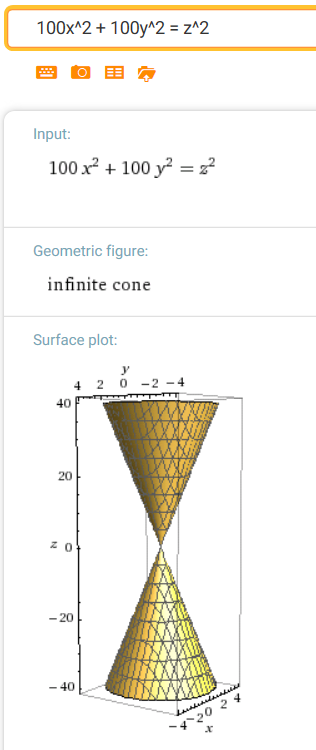
$(10x)^2 + (10y)^2 = z^2$
($\,m = 10\,$)
Observe that when $\,x = 4\,$ and $\,y = 0\,,$
$\,z\,$ is $\,10\cdot 4 = 40\,.$
Equation of a Plane in an $xyz$-Coordinate System
Vector Notation
The notation $\,\langle x,y,z\rangle\,$ denotes the vector from the point $\,(0,0,0)\,$ to the point $\,(x,y,z)\,.$ (Look carefully at the notation: parentheses are used for points, and angle brackets for vectors.)
Notation for Length of a Vector
The length of the arrow representing $\,\vec v = \langle x,y,z\rangle\,$ is denoted by $\,\|\vec v\|\,.$
Formula for Vector From One Point to Another
Let $\,P_1 = (x_1,y_1,z_1)\,$ and $\,P_2 = (x_2,y_2,z_2)\,$ be arbitrary points.
Let $\,\overrightarrow{P_1} = \langle x_1,y_1,z_1\rangle\,$ and $\,\overrightarrow{P_2} = \langle x_2,y_2,z_2\rangle\,$ denote their corresponding vectors.
What is the vector from $\,P_1\,$ to $\,P_2\,$? Denote it, temporarily, by $\,\overrightarrow{P_1P_2}\,.$
By normal vector addition:
$$\overrightarrow{P_1} + \overrightarrow{P_1P_2} = \overrightarrow{P_2}$$(See the idea below, for two-dimensional vectors.)
Solving for $\,\overrightarrow{P_1P_2}\,$ gives:
$$\overrightarrow{P_1P_2} = \overrightarrow{P_2} - \overrightarrow{P_1}$$That is, the vector from $\,(x_1,y_1,z_1)\,$ to $\,(x_2,y_2,z_2)\,$ is:
$$\langle x_2-x_1\,,\,y_2-y_1\,,\,z_2-z_1\rangle$$Just subtract the coordinates: ‘head’ point minus ‘tail’ point!
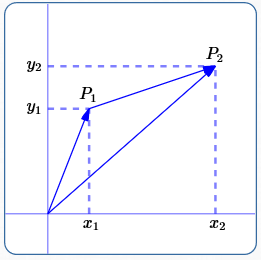
For $\,P_1 = (x_1,y_1)\,$ and $\,P_2 = (x_2,y_2)\,,$
the vector from $\,P_1\,$ to $\,P_2\,$ is:
$
\langle x_2-x_1\,,\,y_2-y_1\rangle
$
Dot Product of Two Vectors
The dot product (or scalar product) of two vectors is defined by:
$$ \langle x_1,y_1,z_1\rangle \cdot \langle x_2,y_2,z_2\rangle := x_1x_2 + y_1y_2 + z_1z_2 $$That is, the dot product of two vectors is the sum of the products of the components.
Alternative Characterization of Dot Product
In (say) a vector calculus class, you'll derive this alternative characterization of the dot product:
$$ \overrightarrow{v_1} \cdot \overrightarrow{v_2} = \|\overrightarrow{v_1}\|\,\|\overrightarrow{v_2}\|\,\cos \theta\,, $$where $\,\theta\,$ is the angle between the two vectors.
This characterization is needed to derive the equation of a plane, as follows.
Dot Product of Perpendicular Vectors
If $\,\overrightarrow{v_1}\,$ and $\,\overrightarrow{v_2}\,$ are perpendicular, then the angle between them is $\,90^\circ\,,$ and $\,\cos 90^\circ = 0\,.$ Thus, when two vectors are perpendicular, their dot product is zero.
The Desired Plane: Known Point and Normal Vector
We seek the equation of a plane $\,\cal P\,$ described as follows:
- Known point: $\,\cal P\,$ contains a known point $\,(x_0,y_0,z_0)$
- Known Normal Vector: Vector $\,\langle a,b,c\rangle\,$ (called a normal vector) is perpendicular to the plane (and hence to every vector in the plane)
A Typical Vector in the Desired Plane
Let $\,(x,y,z)\,$ be any point on $\,\cal P\,$ (see sketch below). The vector from $\,(x_0,y_0,z_0)\,$ to $\,(x,y,z)\,$ is: $$\langle x-x_0,y-y_0,z-z_0\rangle$$
Since both $\,(x_0,y_0,z_0)\,$ and $\,(x,y,z)\,$ lie in $\,\cal P\,,$ so does $\,\langle x-x_0,y-y_0,z-z_0\rangle\,.$
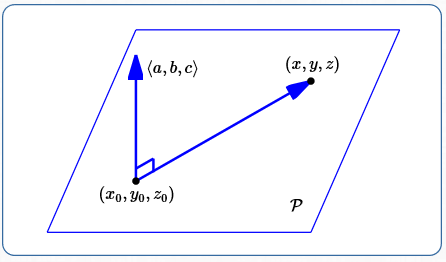
Deriving the Equation of the Plane
Every vector in $\,\cal P\,$ is perpendicular to $\,\langle a,b,c\rangle\,.$ Thus, $\,\langle x-x_0,y-y_0,z-z_0\rangle\,$ is perpendicular to $\,\langle a,b,c\rangle\,.$
Thus:
$$\langle x-x_0,y-y_0,z-z_0\rangle \cdot \langle a,b,c\rangle = 0$$Thus:
$$a(x-x_0) + b(y-y_0) + c(z-z_0) = 0 \qquad (\,\ddagger\,)$$is the equation of the plane through $\,(x_0,y_0,z_0)\,$ with normal vector $\,\langle a,b,c\rangle\,.$
General Equation of a Plane
For the moment, we're only interested in the types of terms in the equation of a plane, not in any particular point on the plane. To this end, multiply out and re-arrange ($\,\ddagger\,$), giving:
$$ ax + by + cz = ax_0 + by_0 + cz_0 $$The right-hand side is just a constant, so give it a simpler name: $\,d := ax_0 + by_0 + cz_0\,.$
Thus, the general equation of a plane with normal vector $\,\langle a,b,c\rangle\,$ is:
$$ ax + by + cz = d \qquad (*) $$Since we want at least one variable to appear (and we need a nonzero normal vector), at least one of $\,a\,,$ $\,b\,,$ and $\,c\,$ must be nonzero.
Note that the only types of terms that planes are allowed to have are $\,x\,,$ $\,y\,,$ $\,z\,,$ and constant terms.
To emphasize: when the $\,x\,,$ $\,y\,$ and $\,z\,$ terms are all on the same side of the equation, then
$$\langle \, \text{coefficient of $\,x\,$}\, ,\, \text{coefficient of $\,y\,$}\, ,\, \text{coefficient of $\,z\,$}\rangle$$is a normal vector to the plane.
Below are some WolframAlpha plots of planes. Take a few moments to think about each of the normal vectors!

$x + y + z = 0$
normal vector: $\,\langle 1,1,1\rangle$
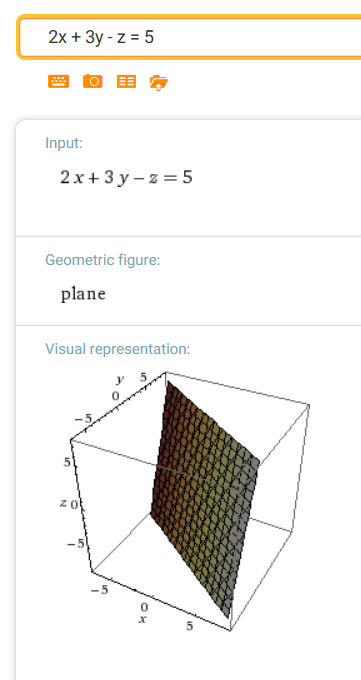
$2x + 3y - z = 5$
normal vector: $\,\langle 2,3,-1\rangle$
$x = 5$
normal vector: $\,\langle 5,0,0\rangle$
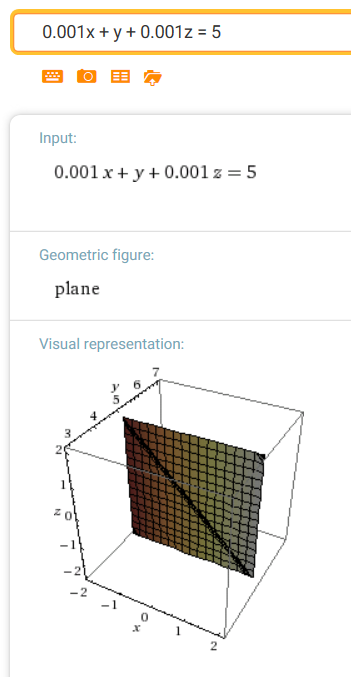
$y = 5$
normal vector: $\,\langle 0,5,0\rangle$
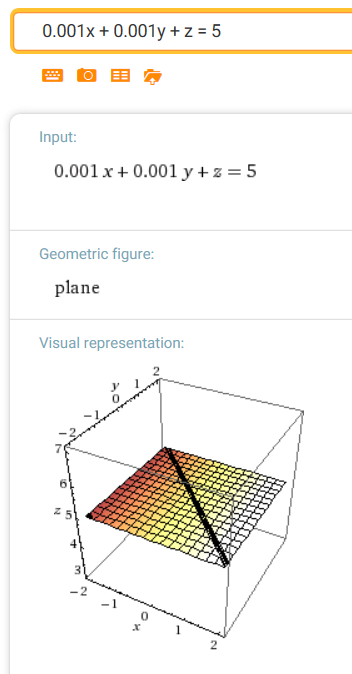
$z = 5$
normal vector: $\,\langle 0,0,5\rangle$
Note: To help WolframAlpha realize we want an equation in three variables, we put in very small coefficients for the missing terms.
Thus, for example, we input:
x + 0.001y + 0.001z = 5
instead of just:
x = 5
Intersect an Infinite Double Cone and a Plane
Next, we want to find the intersection of:
- an infinite double cone: $\,(mx)^2 + (my)^2 = z^2\,$
- a plane: $\,ax + by + cz = d\,$
So, proceed as follows:
(1) At least one of $\,a\,,$ $\,b\,$ or $\,c\,$ is nonzero. Assuming $\,c\ne 0\,,$ solve the plane equation for $\,z\,$:
$$ z = \frac{d - ax - by}{c} $$(2) Substitute the expression from (1) into the equation of the infinite double cone:
$$ (mx)^2 + (my)^2 = \left( \frac{d - ax - by}{c}\right)^2 $$(3) Simplify and re-arrange:
$$ (mx)^2 + (my)^2 = \left( \frac{d - ax - by}{c}\right)^2 $$$$ \begin{align} &c^2m^2x^2 + c^2m^2y^2 \cr &\quad = (d-ax-by)(d-ax-by) \end{align} $$
$$ \begin{align} &c^2m^2x^2 + c^2m^2y^2\cr &\quad = d^2 - adx - bdy\cr &\qquad - adx + a^2x^2 + abxy\cr &\qquad - bdy + abxy + b^2y^2 \end{align} $$
$$ \begin{align} &c^2m^2x^2 + c^2m^2y^2\cr &\quad = d^2 - 2adx - 2bdy\cr &\qquad + a^2x^2 + 2abxy + b^2y^2 \end{align} $$
$$ \begin{align} &\color{red}{x^2}(c^2m^2 - a^2) + \color{red}{xy}(-2ab) + \color{red}{y^2}(c^2m^2 - b^2)\cr &\quad + \color{red}{x}(2ad) + \color{red}{y}(2bd) - d^2 = 0 \quad (**) \end{align} $$
(Note: See what equations result if you assume $\,a\ne 0\,$ or $\,b\ne 0\,.$ )
The Intersection of an Infinite Double Cone and a Plane is an Equation With Only $\,x^2\,,$ $\,xy\,,$ $\,y^2\,,$ $\,x\,,$ $\,y\,,$ and Constant Terms
Look carefully at equation (**).
The only types of terms it is allowed to have are $\,x^2\,,$ $\,xy\,,$ $\,y^2\,,$ $\,x\,,$ $\,y\,,$ and constant terms.
Thus, the intersection of an infinite double cone and a plane gives rise to an equation of the form:
$$Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0$$Note: Equation (**) actually describes the projection onto the $xy$-plane of the intersection of the infinite double cone and the slicing plane. It does not describe the curve in the slicing plane. However, this derivation hopefully makes it plausible that the actual intersection has the desired form.
Here's an alternative approach, inspired by my genius husband Ray, that avoids the projection difficulty and shows that the actual equation is of the desired form. This way rotates/translates the cone so that the slicing plane aligns with the $\,xy\,$ plane ($\,z = 0\,$). An outline of the approach follows.
Alternative Approach
Imagine the double infinite cone with a slicing plane. In your mind's eye, make it all rigid—so you can grab the plane/cone figure and move it around.
For example, you might imagine the plane as a board that has been ‘glued into place’ in its slicing position; the edges of the board become handles that you can hold on to, to move the whole thing around!
Let $\,x\,$ be left/right, $\,z\,$ up/down, and $\,y\,$ straight in front of you (and back).
Here's what you need to convince yourself of: with only three types of actions (listed below), you can lay the board flat on your table top (which we'll call the $\,z = 0\,$ level):
- Rotate the cone about the $z$-axis (i.e., spin it like a top)
- Rotate the cone about the $y$-axis (i.e., tip it left/right)
- Move the cone up/down
Here's how these three movements affect the equation of the cone:
Rotation About the $z$-axis
This movement doesn't change the $\,z\,$-values; it causes a rotation in planes parallel to the $\,xy\,$-plane. Any rotation about the origin in an $\,xy\,$ plane can be accomplished by:
- replacing every $\,x\,$ in the equation by $\,ax+by$
- replacing every $\,y\,$ in the equation by $\,cx+dy$
For our purposes here, the actual coefficients don't matter—we're only interested in the types of terms that result. For more details, see the rotation discussion in the next section.
Notice that, for simplicity here, we're not distinguishing between original variables (like $\,x\,$) and transformed variables (like $\,\hat x\,$).
Rotation About the $y$-axis
This movement doesn't change the $y$-values; it causes a rotation in planes parallel to the $\,xz\,$ plane. Any rotation about the origin in the $\,xz\,$ plane can be accomplished by:
- replacing every $\,x\,$ in the equation by $\,ex+fz$
- replacing every $\,z\,$ in the equation by $\,gx+hz$
Movement Up/Down
Moving up/down is just translation: replace every $\,z\,$ by $\,z + k\,.$
Apply These Transformations to the Cone
So, there exist appropriate constants $\,a\,,$ $\,b\,,$ $\,c\,,$ $\,d\,,$ $\,e\,,$ $\,f\,,$ $\,g\,,$ $\,h\,$ and $\,k\,$ that will move the slicing plane to the $\,z = 0\,$ level.
Apply these transformations to the cone $\,m^2x^2 + m^2y^2 = z^2\,$:
$$ \begin{gather} m^2(ax+by)^2 + m^2(cx+dy)^2 = z^2 \end{gather} $$(rotation about $z$-axis)
$$ \begin{align} &m^2(a(ex+fz)+by)^2\cr &\quad + m^2(c(ex+fz)+dy)^2\cr &= (gx+hz)^2 \end{align} $$
(rotation about $y$-axis)
$$ \begin{align} &m^2(a(ex+f(z+k))+by)^2\cr &\quad + m^2(c(ex+f(z+k))+dy)^2\cr &= (gx+h(z+k))^2 \end{align} $$
(moving up/down)
The Intersecting Plane is Now At $\,z = 0$
The intersection of the double infinite cone and the plane is found by setting $\,z = 0\,$ (since the desired curve is now the intersection of the transformed cone with the table top):
$$ \begin{align} &m^2(a(ex+f(0+k))+by)^2\cr &\quad + m^2(c(ex+f(0+k))+dy)^2\cr &= (gx+h(0+k))^2 \end{align} $$$$ \begin{align} &m^2(a(ex+fk)+by)^2\cr &\quad + m^2(c(ex+fk)+dy)^2\cr &= (gx+hk)^2 \end{align} $$
$$ \begin{align} &m^2(aex+afk+by)^2\cr &\quad + m^2(cex+cfk+dy)^2\cr &= (gx+hk)^2 \end{align} $$
Mentally multiply this out—what term types arise? Only $\,x^2\,,$ $\,xy\,,$ $\,y^2\,,$ $\,x\,,$ $\,y\,$ and constants!
One of my website users used Paint 3D to intersect the cone with a plane, and then drag that plane to the ‘tabletop’. This is what he saw! (I''m posting his image with permission—thanks, Michael B!)
