This section is optional in the Precalculus course. There are no exercises in this section.
This section addresses a question about conics which may have arisen as you studied Identifying Conics by the Discriminant:
The purpose of this section is not to give a complete answer to this question. Instead, the purpose is to give enough information—at a level within the grasp of an ambitious Precalculus student—to make the answer plausible.
Here's the situation (summarized from Identifying Conics by the Discriminant):
-
Every equation of the form
$\,Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0\,$ graphs as a conic, a degenerate conic,
or a curve that arises from a ‘limiting case’ of an infinite double cone.
This is referred to as the (standard form of) the general conic equation. - The expression $\,B^2 - 4AC\,$ is called the (conic) discriminant.
If $\,B^2 - 4AC < 0\,,$ the general conic equation graphs as an ellipse (possibly degenerate).
If $\,B^2 - 4AC = 0\,,$ the general conic equation graphs as a parabola (possibly degenerate).
If $\,B^2 - 4AC > 0\,,$ the general conic equation graphs as a hyperbola (possibly degenerate).
That is, why does $\,B^2 - 4AC\,$ give this information?
Keep reading!
Here's the overview of what we'll do in this optional section:
-
Use an equivalent definition of conic sections
to get simple standard forms for ellipses, parabolas, and hyperbolas. - Show that these simple standard forms have the desired discriminants:
negative for ellipse, zero for parabola, positive for hyperbola. - Show that every general conic equation can be transformed to one of these simple standard forms
using only (as needed) a rotation and/or horizontal/vertical translations. - Show that the discriminant is invariant (i.e., doesn't change) under translations and rotation.
So, the discriminant of the original general conic equation and the (transformed) simple standard form are the same!
At this point, you'll be able to say:
But—where did it come from? How did someone think to look at this particular expression?
The details follow:
Equivalent Definitions of Conics
There are equivalent definitions of conics:
- plane-intersecting-cone definition
In Introduction to Conic Sections, this definition was introduced.
It says that conics arise as the intersection of an infinite double cone and a plane.
- alternate definitions
In the next few sections, alternate definitions of ellipse, parabola, and hyperbola are discussed,
which facilitate easy derivation of standard forms for each type of conic section.
- equivalence of definitions
The equivalence of these definitions can be proven using Dandelin spheres.
Summary: Standard Forms of Conics
The table below summarizes the standard forms for the conics—they'll all be derived in subsequent sections.
These standard forms position the conics in an $\,xy\,$-coordinate system so that the simplest possible equations result.
| CONIC | STANDARD FORM(S) | COMPUTATION OF DISCRIMINANT, $\,B^2 - 4AC\,$
With all three terms on the same side of the equation:
$\,A\,$ is the coefficient of the $\,x^2\,$ term $\,B\,$ is the coefficient of the $\,xy\,$ term $\,C\,$ is the coefficient of the $\,y^2\,$ term |
| ellipse | $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$ | $\displaystyle A = \frac{1}{a^2}\,,$ $B = 0\,,$ $\displaystyle C = \frac{1}{b^2}\,$ $$ \begin{align} B^2 - 4AC \ \ &=\ \ 0^2 - 4\cdot\frac{1}{a^2}\cdot\frac{1}{b^2}\cr &= \frac{-4}{a^2\,b^2}\cr\cr &< 0 \end{align} $$ |
| parabola | $$x^2 = 4py$$ or $$y^2 = 4px$$ |
$A = 1\,,$
$B = 0\,,$
$C = 0\,$
$$
B^2 - 4AC \ \ =\ \ 0^2 - 4(1)(0)\ \ =\ \ 0
$$
or $A = 0\,,$ $B = 0\,,$ $C = 1\,$ $$ B^2 - 4AC \ \ =\ \ 0^2 - 4(0)(1)\ \ =\ \ 0 $$ |
| hyperbola | $$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$ or $$\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1$$ |
$\displaystyle A = \frac{1}{a^2}\,,$
$B = 0\,,$
$\displaystyle C = -\frac{1}{b^2}\,$
$$
B^2 - 4AC \ \ =\ \ 0^2 - 4\cdot\frac{1}{a^2}\cdot\frac{-1}{b^2}\ \
= \frac{4}{a^2\,b^2}\ \ >\ \ 0
$$
or $\displaystyle A = -\frac{1}{b^2}\,,$ $B = 0\,,$ $\displaystyle C = \frac{1}{a^2}\,$ $$ B^2 - 4AC \ \ =\ \ 0^2 - 4\cdot\frac{-1}{b^2}\cdot\frac{1}{a^2}\ \ = \frac{4}{a^2\,b^2}\ \ >\ \ 0 $$ |
The Standard Forms have the Expected Discriminants
Notice, from the table above, that the standard forms have the expected discriminants:
| ellipses: | $\,B^2 - 4AC < 0$ |
| parabolas: | $\,B^2 - 4AC = 0$ |
| hyperbolas: | $\,B^2 - 4AC > 0$ |
Every general conic equation can be transformed to a standard form
Every general conic equation can be transformed to a standard form,
using only (as needed) a rotation and/or horizontal/vertical translations.
None of the standard forms have an $\,xy\,$ term.
Therefore, we need to get rid of the $\,xy\,$ term from the general conic equation.
An appropriate rotation of the graph will do the job, as shown below.
After the $\,xy\,$ term is gone, horizontal/vertical translation(s) will give the desired standard form.
Rotating a Graph
| Given a graph, we seek a new equation which describes
the same graph—except that the graph is rotated counterclockwise by an angle $\,\theta\,.$ The necessary ‘rotation equations’ follow easily from two things:
|
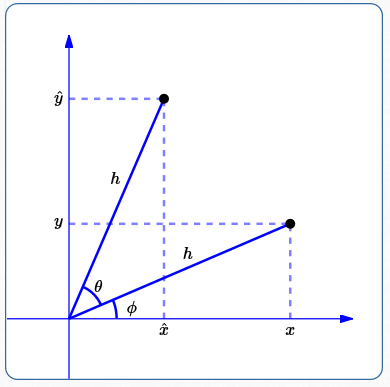 |
Next, the equations $$\begin{gather} \hat x = x\cos\theta - y\sin\theta\qquad (1)\cr \hat y = y\cos\theta + x\sin\theta\qquad (2) \end{gather} $$ are solved for $\,x\,$ and $\,y\,$ (in terms of $\,\hat x\,$ and $\,\hat y\,$), as follows.
To eliminate $\,y\,$:
- Multiply both sides of (1) by $\,\cos\theta\,.$
- Multiply both sides of (2) by $\,\sin\theta\,.$
- This gives: $$\begin{gather} \hat x\cos\theta = x\cos^2\theta - y\sin\theta\cos\theta\cr \hat y\sin\theta = x\sin^2\theta + y\sin\theta\cos\theta \end{gather} $$
- Adding the left and right sides of these two equations gives the expression for $\,x\,$: $$ \hat x\cos\theta + \hat y\sin\theta = x(\cos^2\theta + \sin^2\theta) = x $$
- Proceed similarly (eliminating $\,x\,$) to get the equation for $\,y\,$: $$ y = \hat y\cos\theta - \hat x\sin\theta $$
Thus, we have:
To rotate a graph counterclockwise by an angle $\,\theta\,$
$x = \hat x\cos\theta + \hat y\sin\theta$
$y = \hat y\cos\theta - \hat x\sin\theta$
Suppose you have a graph, which is the solution set of a known equation in $\,x\,$ and $\,y\,.$
- In the known equation for the graph:
replace every $\,x\,$ by: $\,\hat x\cos\theta + \hat y\sin\theta\,$ replace every $\,y\,$ by: $\,\hat y\cos\theta - \hat x\sin\theta$ - At this point, you have an equation in the variables $\,\hat x\,$ and $\,\hat y\,.$
Graph it, just as you would if its variables were $\,x\,$ and $\,y\,.$
This new graph will be identical to the original graph, except rotated counterclockwise by $\,\theta\,.$
A Simple Rotation Example
Here's a simple example to illustrate the idea.
If the line $\,y = x\,$ is graphed in a coordinate system where the scales on $\,x\,$ and $\,y\,$ are identical,
then it graphs as a line that makes a $\,45^\circ\,$ angle with the positive $\,x\,$-axis.
If this line is rotated by $\,45^\circ\,$ counterclockwise, then it ‘turns into’ the $y$-axis: i.e., the line $\,x = 0\,.$
Here are the steps in transforming the equation:
- Start with $\,y = x\,$ (the original equation).
- We want $\,\theta = 45^\circ\,.$
Thus, $\,\sin\theta = \frac{1}{\sqrt 2}\,$ and $\,\cos\theta = \frac{1}{\sqrt 2}\,.$ - In the original equation, replace:
- $\,x\,$ by $\,\hat x\cos\theta + \hat y\sin\theta = \hat x\cdot\frac 1{\sqrt 2} + \hat y\cdot\frac1{\sqrt 2}$
- $\,y\,$ by $\,\hat y\cos\theta - \hat x\sin\theta = \hat y\cdot\frac 1{\sqrt 2} - \hat x\cdot\frac1{\sqrt 2}$
- These replacements give: $$ \begin{gather} y = x\cr\cr \hat y\cdot\frac{1}{\sqrt 2} - \hat x\cdot\frac{1}{\sqrt 2} = \hat x\cdot \frac{1}{\sqrt 2} + \hat y\cdot\frac{1}{\sqrt 2}\cr\cr \text{Simplify to get:}\cr\cr \hat x = 0 \end{gather} $$
- Observe that the resulting equation is $\,\hat x = 0\,.$
The different variable ($\,\hat x\,$ instead of $\,x\,$) reminds you that this is a different equation than what you started with:
it has been rotated by $\,45^\circ\,$ counterclockwise!
Rotate the General Conic Equation to Eliminate the $\,xy\,$ Term
Next, we apply the rotation equations to the general conic equation, $\,Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0\,.$
The goal is to determine an appropriate angle of rotation, $\,\theta\,,$ that will eliminate the $\,xy\,$ term.
- Rotate the general conic equation by $\,\theta\,$: $$A(\hat x\cos\theta + \hat y\sin\theta)^2 + B(\hat x\cos\theta + \hat y\sin\theta)(\hat y\cos\theta - \hat x\sin\theta) + C(\hat y\cos\theta - \hat x\sin\theta)^2 + D(\hat x\cos\theta + \hat y\sin\theta) + E(\hat y\cos\theta - \hat x\sin\theta) + F = 0 $$
- The term $\,\hat x\hat y\,$ can only arise from the terms that begin with $\,A\,,$ $\,B\,,$ and $\,C\,.$
Mentally multiplying things out, the coefficient of the $\,\hat x\hat y\,$ term is: $$A(2\sin\theta\cos\theta) + B(\cos^2\theta - \sin^2\theta) + C(-2\sin\theta\cos\theta) $$ - We seek $\,\theta\,$ so that the $\,\hat x\hat y\,$ term disappears, so set its coefficient to zero: $$A(2\sin\theta\cos\theta) + B(\cos^2\theta - \sin^2\theta) + C(-2\sin\theta\cos\theta) = 0 $$
- This equation is not easy to solve for $\,\theta\,$ in its current form.
So, use the trigonometric identities $$ \begin{gather} 2\sin\theta\cos\theta = \sin 2\theta\cr\cr \cos^2\theta - \sin^2\theta = \cos 2\theta\cr\cr \tan\theta = \frac{\sin\theta}{\cos\theta} \end{gather} $$ to simplify the equation, as follows: $$ \begin{gather} A\sin 2\theta + B\cos 2\theta - C\sin 2\theta = 0\cr\cr (A-C)\sin 2\theta = -B\cos 2\theta \qquad (\dagger)\cr\cr \text{Assuming $\,A\ne C\,$:}\cr\cr \frac{\sin 2\theta}{\cos 2\theta} = \frac{-B}{A-C} = \frac{B}{C-A}\cr\cr \tan 2\theta = \frac{B}{C - A} \end{gather} $$ - This equation can now easily be solved for $\,\theta\,$ by using the arctangent function: $$\begin{gather} 2\theta = \arctan{\left(\frac{B}{C-A}\right)}\cr\cr \theta = \frac 12\arctan{\left(\frac{B}{C-A}\right)}\,, \quad \text{for} \quad A\ne C \end{gather} $$
- What happens if $\,A = C\,$?
Take a look at equation ($\,\dagger\,$).
If $\,A = C\,,$ then the left side of the equation is zero.
In order for the equation to be true, the right side must also be zero: so either $\,B = 0\,$ or $\,\cos 2\theta = 0\,.$
If $\,B = 0\,,$ then the original conic equation doesn't have an $\,xy\,$ term—so no rotation is needed!
If $\,\cos 2\theta = 0\,,$ then the smallest positive angle that works is $\,2\theta = 90^\circ\,,$ so $\,\theta = 45^\circ\,.$ - Note that, since the arctangent always returns
an angle strictly between $\,-90^\circ\,$ and $\,90^\circ\,,$
the angle $\,\theta = \frac 12\arctan{\left(\frac{B}{C-A}\right)}\,$ always lies between $\,-45^\circ\,$ and $\,45^\circ\,.$ - For our purposes, here is the critical observation:
Every general conic equation $\,Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0\,$
can be rotated by an appropriate angle
so that the $\,xy\,$ term is eliminated.
With No $\,xy\,$ Term in the General Conic Equation,
Appropriate Translation(s) Will Always Produce the Standard Forms
After an appropriate rotation, we'll have a new conic equation in $\,\hat x\,$ and $\,\hat y\,$ that has no $\,\hat x\hat y\,$ term:
$$\tilde A \hat x^2 + \tilde C \hat y^2 + \tilde D \hat x + \tilde E\hat y + \tilde F = 0
$$
The other coefficients likely all have changed in the process.
This equation looks unnecessarily complicated, with all the ‘hats’ ($\,\hat{}\,$) and ‘tildes’ ($\,\tilde{}\,$).
For simplicity, let's drop them all and instead investigate the equation:
$$Ax^2 + Cy^2 + Dx + Ey + F = 0 \qquad (\ddagger)$$
Use the completing the square technique to get perfect squares involving $\,x\,$ and $\,y\,$:
- If both $\,A\ne 0\,$ and $\,C\ne 0\,$ in ($\,\ddagger\,$):
$$
\begin{gather}
A\left(x^2 + \frac DAx + \left(\frac{D}{2A}\right)^2\right)
+ C\left(y^2 + \frac ECy + \left(\frac{E}{2C}\right)^2\right) = -F + A\left(\frac{D}{2A}\right)^2 + C\left(\frac{E}{2C}\right)^2\cr\cr
A\left(x+\frac D{2A}\right)^2 + C\left(y + \frac{E}{2C}\right)^2 = -F + \frac{D^2}{4A} + \frac{E^2}{4C}
\end{gather}
$$
Replacing every $\,x\,$ by $\,x - \frac{D}{2A}\,$ (horizontal translation)
and every $\,y\,$ by $\,y - \frac{E}{2C}\,$ (vertical translation)
then gives an equation of the form $\,Ax^2 + Cy^2 = \text{constant}\,,$
which is easily adjusted to either an ellipse or hyperbola in standard form. - If $\,A\,$ and $\,C\,$ are both zero in ($\,\ddagger\,$), then no translations are needed—the graph is a line (a degenerate case of a parabola).
- If $\,A\ne 0\,,$ $\,C = 0\,,$ and $\,E \ne 0\,$ in ($\,\ddagger\,$), then:
$$\begin{gather}
A\left(x^2 + \frac DAx + \left(\frac{D}{2A}\right)^2\right)
= -Ey - F + \frac{D^2}{4A}\cr\cr
A\left(x+\frac D{2A}\right)^2 = -E(y + \frac FE - \frac{D^2}{4AE})
\end{gather}
$$
Replacing every $\,x\,$ by $\,x - \frac{D}{2A}\,$ (horizontal translation)
and every $\,y\,$ by $\,y -\frac FE + \frac{D^2}{4AE}\,$ (vertical translation)
then gives an equation of the form $\,Ax^2 = -Ey\,,$ which is easily adjusted to a parabola in standard form. - The remaining cases are similar to those above.
For our purposes, the critical observation is this:Every general conic equation $\,Ax^2 + Cy^2 + Dx + Ey + F = 0\,$ with no $\,xy\,$ term
can be translated appropriately to produce one of the standard forms for conics.
The Conic Discriminant is Invariant Under Translations
When the general conic equation is translated (horizontally and/or vertically), a new equation results.
However, the original equation and the new (translated) equation will have exactly the same discriminant!
To see this, replace every $\,x\,$ by $\,x - c\,$ and every $\,y\,$ by $\,y - d\,$ in the general conic equation,
and then focus attention on the degree-two terms:
$$
\begin{gather}
A(x-c)^2 + B(x-c)(y-d) + C(y-d)^2 + D(x-c) + E(y - d) + F = 0\cr\cr
Ax^2 + Bxy + Cy^2 + \hat D x + \hat Ey + \hat F = 0
\end{gather}
$$
Note that the coefficients of the degree-two terms haven't changed!
Thus, the discriminant is invariant under translations.
The Conic Discriminant is Invariant Under Rotation
When the general conic equation is rotated, a new equation results.
However, the original equation and the new (rotated) equation will have exactly the same discriminant!
To see this, use the rotation equations in the general conic equation, and focus attention on the degree-two terms.
For simplicity, let $\,c := \cos\theta\,$ and $\,s := \sin\theta\,.$
$$
\begin{gather}
A(\hat xc + \hat ys)^2 + B(\hat xc + \hat ys)(\hat yc - \hat xs) + C(\hat yc - \hat xs)^2 + \text{(non-degree-two stuff)} = 0\cr\cr
\text{(drop the hats on the variables, for simplicity)}\cr\cr
A(c^2x^2 + 2csxy + s^2y^2)
+ B(c^2xy - csx^2 + csy^2 - s^2xy)
+ C(c^2y^2 - 2csxy + s^2x^2) + \text{non-degree-two terms} = 0\cr\cr
x^2(Ac^2 - Bcs + Cs^2)
+ xy(2Acs + Bc^2 - Bs^2 - 2Ccs)
+ y^2(As^2 + Bcs + Cc^2) + \text{non-degree-two terms} = 0\cr\cr
\end{gather}
$$
For this new (rotated) equation, the degree-two coefficients are:
$$
\begin{align}
\hat A &= Ac^2 - Bcs + Cs^2\cr\cr
\hat B &= B(c^2-s^2) + 2cs(A - C)\cr\cr
\hat C &= As^2 + Bcs + Cc^2
\end{align}
$$
At this point, it's an exercise in patience and being careful!
Here's the new discriminant:
$$
\begin{align}
\hat B^2 - 4\hat A\hat C &= \bigl(B(c^2-s^2) + 2cs(A - C)\bigr)^2 - 4(Ac^2 - Bcs + Cs^2)(As^2 + Bcs + Cc^2)\cr\cr
&= B^2(c^2-s^2)^2 + 4Bcs(c^2-s^2)(A-C) + 4c^2s^2(A-C)^2 \cr
&\qquad \qquad \qquad -4(A^2c^2s^2 + ABc^3s + ACc^4 - ABcs^3 - B^2c^2s^2 - BCc^3s + ACs^4 + BCcs^3 + C^2c^2s^2)\cr\cr
&= B^2(c^4 - 2c^2s^2 + s^4) + 4Bcs(Ac^2 - Cc^2 - As^2 + Cs^2) + 4c^2s^2(A^2 - 2AC + C^2)\cr
&\qquad \qquad \qquad -4A^2c^2s^2 - 4ABc^3s - 4ACc^4 + 4ABcs^3 + 4B^2c^2s^2 + 4BCc^3s - 4ACs^4 - 4BCcs^3 - 4C^2c^2s^2\cr\cr
&= B^2c^4 \color{green}{- 2B^2c^2s^2} + B^2s^4 \color{orange}{\cancel{+ 4ABc^3s}} \color{grey}{\cancel{\bcancel{- 4BCc^3s}}} \color{purple}{\bcancel{- 4ABcs^3}} \color{red}{\bcancel{\cancel{+ 4BCcs^3}}} \color{blue}{\bcancel{+ 4A^2c^2s^2}} - 8ACc^2s^2 + \color{pink}{\cancel{4C^2c^2s^2}}\cr
&\qquad \qquad \qquad \color{blue}{\bcancel{- 4A^2c^2s^2}} \color{orange}{\cancel{- 4ABc^3s}} - 4ACc^4 \color{purple}{\bcancel{+ 4ABcs^3}} \color{green}{+ 4B^2c^2s^2} \color{grey}{\cancel{\bcancel{+ 4BCc^3s}}} - 4ACs^4 \color{red}{\bcancel{\cancel{- 4BCcs^3}}} \color{pink}{\cancel{- 4C^2c^2s^2}}\cr\cr
&= B^2c^4 - 4ACc^4 + 2B^2c^2s^2 - 8ACc^2s^2 + B^2s^4 - 4ACs^4 \cr\cr
&= c^4(B^2 - 4AC) + 2c^2s^2(B^2-4AC) + s^4(B^2-4AC)\cr\cr
&= (B^2 - 4AC)(c^4 + 2c^2s^2 + s^4)\cr\cr
&= (B^2 - 4AC)(\cos^2 \theta + \sin^2\theta)^2\cr\cr
&= B^2 - 4AC
\end{align}
$$
Whew!
So, the discriminant of the new (rotated) equation is the same as the original discriminant.
Thus, the discriminant is invariant under rotation.
How Did Someone Know to Look at This Particular Expression, $\,B^2 - 4AC\,$?
At this point, you should understand why the discriminant, $\,B^2 - 4AC\,,$ can be used
to identify
the type of conic you get from the equation $\,Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0\,.$
However, you might still be wondering—how did someone think to look at this particular expression?
Here's one way that (say) an inquisitive student might have stumbled upon the suspected importance of $\,B^2 - 4AC\,.$
First, re-name the expression $\,Ax^2 + Bxy + Cy^2\,$ by completing the square on the first two terms.
(This re-writing requires $\,A\ne 0\,.$ )
$$
\begin{alignat}{2}
Ax^2 + Bxy + Cy^2 &= Ax^2 + (By)x + Cy^2 &\qquad&\text{(treat $\,By\,$ as the coefficient of the $\,x\,$ term)}\cr\cr
&= A(x^2 + \frac{By}{A}x \qquad) + Cy^2 &&\text{(completing the square requires the coefficient of $\,x^2\,$ to be $\,1\,$)}\cr\cr
&= A\left(x^2 + \frac {By}{A}x + \left(\frac{By}{2A}\right)^2\right) + Cy^2 - A\left(\frac{By}{2A}\right)^2 &&\text{(add half the $\,x\,$ coefficient, squared; add zero in appropriate form)} \cr\cr
&= A\left(x + \frac{By}{2A}\right)^2 + y^2\left(C - \frac{B^2}{4A}\right)&&\text{(write first expression as a perfect square; factor out $\,y^2\,$)}\cr\cr
&= A\left(x + \frac{B}{2A}y\right)^2 + y^2\left(\frac{4AC}{4A} - \frac{B^2}{4A}\right)&&\text{(get common denominator)}\cr\cr
&= A\left(x + \frac{B}{2A}y\right)^2 - \frac{y^2}{4A}(B^2 - 4AC)&&\text{(algebra)}\cr\cr
\end{alignat}
$$
Use this new name to explore the conic equation with only degree-two terms:
$$
\begin{gather}
Ax^2 + Bxy + Cy^2 = 0\cr\cr
A\left(x + \frac{B}{2A}y\right)^2 - \frac{y^2}{4A}(B^2 - 4AC) = 0\cr\cr
\color{green}{4A^2\left(x + \frac{B}{2A}y\right)^2} - \color{red}{y^2}(B^2 - 4AC) = 0\cr\cr
\end{gather}
$$
Since the green and red parts are always nonnegative,
the nature of the equation
changes
significantly depending upon whether $\,B^2-4AC\,$ is positive, negative, or zero!
Note: If you assume $\,C\ne 0\,,$ and complete the square on $\,y\,,$ you reach the same conclusion.
Move on to the next lesson:
Parabolas: Definition, Reflectors/Collectors, Derivation of Equations