This multiplication trick was posted on Facebook. Here's why it works (and what its limitations are). The images below are from the original link.

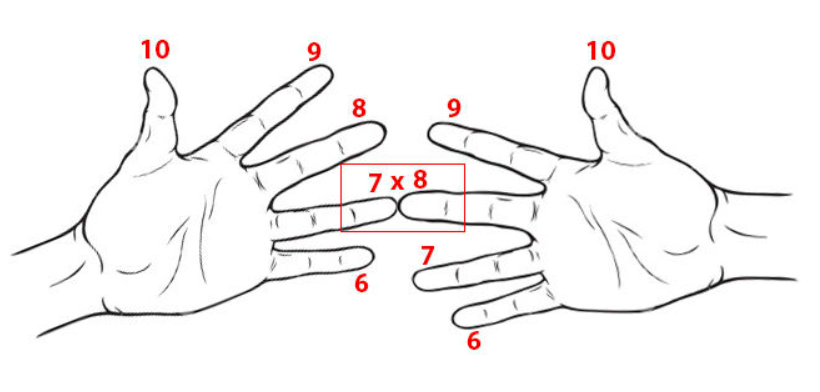
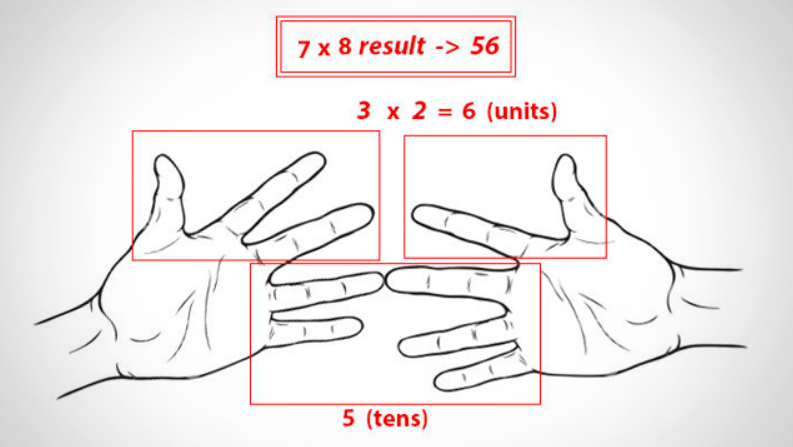
In case the link above breaks, here's the trick:

• Hold your hands, with palms facing you (first image above).
• On each hand, number the fingers 6 through 9 (from the bottom up; pinky to index finger).
• Touch the fingers you want to multiply: for example, to multiply 6 by 9, touch the pinky on one hand to the index finger on the other hand.
• COUNT the two fingers that touch, plus any fingers below; this sum becomes the TENS digits in the product (Second image above; bottom red box)
• COUNT the fingers above the touching fingers on the left. COUNT the fingers above the touching fingers on the right. MULTIPLY these two (small) numbers together. This becomes the ONES digit in the product. (Second image above; top two red boxes)

Here's Why It Works:

Suppose you want to multiply $\,x\,$ by $\,y\,,$ where these two numbers are $\,6\,,$ $\,7\,,$ $\,8\,,$ or $\,9\,.$ That is, you want to find the product $\,xy\,.$

• The number of fingers strictly below $\,x\,$ is $\,x - 6\,.$ For example, if $\,x = 6\,$ then there are $\,x - 6 = 6 - 6 = 0\,$ fingers below. If $\,x = 7\,,$ there is $\,x - 6 = 7 - 6 = 1\,$ finger below.
• The number of fingers strictly above $\,x\,$ is $\,10 - x\,.$ For example, if $\,x = 6\,$ then there are $\,10 - x = 10 - 6 = 4\,$ fingers above. If $\,x = 7\,,$ there are $\,10 - x = 10 - 7 = 3\,$ fingers above.
• The SUM OF THE FINGERS strictly below, plus the two fingers that are touching, is: $$ \begin{gather} (x-6) + (y - 6) + 2\ \ =\ \ x + y - 10 \cr \text{(SumOnAndBelow)} \end{gather} $$ Observe that $\,x + y - 10\,$ is always between $\,2\,$ and $\,8\,$ when $\,x\,$ and $\,y\,$ only take on values in the set $\,\{6,7,8,9\}\,.$ In particular,  SumOnAndBelow  is always a single-digit number.
• The PRODUCT OF THE FINGERS strictly above is $$ \begin{gather} (10-x)(10-y)\cr (\text{ProductAbove}) \end{gather} $$ Unfortunately, this is not always a single-digit number! If $\,x = 6\,$ and $\,y = 6\,,$ then we get (for example) $\,(10-6)(10-6) = 16\,.$ Or, if $\,x = 6\,$ and $\,y = 7\,$ (or vice versa), then we get $\,(10-6)(10-7) = 4\cdot 3 = 12\,.$ All other combinations do indeed give a single-digit number.
• They want us to put the  SumOnAndBelow  digit in the tens place. How much does this contribute to the final number? Answer: $$10\cdot(\text{SumOnAndBelow}) = 10(x+y - 10)$$
• So, here's why this works (when  ProductAbove  is a single-digit number): $$ \begin{align} 10(&\text{SumOnAndBelow}) + \text{ProductAbove}\cr &= \ \ 10(x+y-10) + (10-x)(10-y)\cr &=\ \ 10x + 10y - 100 + 100 - 10x - 10y + xy\cr &=\ \ xy \end{align} $$ Cool! I love it!

How to Handle the Exceptions—an Easy ‘Carry’

The exceptions ($\,6\cdot 6\,$ and $\,6\cdot 7\,$) aren't much harder. Take the extra ‘$\,1\,$’ from the product, and add it to the sum, like this:

$6\cdot 6\,$:

• $\text{SumOnAndBelow} = 2$
• $\text{ProductAbove} = 4\cdot 4 = \color{red}{1}6$
• Take the ‘$\,\color{red}{1}\,$’ from the tens place and add it to the $\,2\,,$ giving $\,3\,.$
• Result: $\,36\,$

$6\cdot 7\,$:

• $\text{SumOnAndBelow} = 3$
• $\text{ProductAbove} = 4\cdot 3 = \color{red}{1}2$
• Take the ‘$\,\color{red}{1}\,$’ from the tens place and add it to the $\,3\,,$ giving $\,4\,.$
• Result: $\,42\,$

Why?

If the product $\,(10-x)(10-y)\,$ is a two-digit number, then when you subtract $\,10\,,$ the result is a one-digit number. So, add zero in the form ‘$\,10 - 10\,$’, as follows: