Revisiting ‘Equal’ versus ‘Approximately Equal’

(This section is optional in the Precalculus course. It can be skipped without any loss of continuity. There are no exercises in this section.)

If you (like me) want everything to be ‘just perfect’ in your mathematical world, then you may have been bothered by the usage of ‘$\,=\,$’ (equal) and ‘$\,\approx\,$’ (approximately equal) in the example of the previous section . (No need to go back—it's repeated below for your convenience.)

If so, hopefully this section will put you a bit more at ease.

If you've been going through my entire online curriculum, then you already know that I'm picky about distinguishing between equal versus approximately equal. In most cases, I abide by this motto:

Don't say two things are equal unless they truly are equal. If they're only approximately equal, use ‘$\,\approx\,$’.

There are, however, situations where this motto should probably not be followed. Why not? Because strict adherence can make a simple problem look absolutely hideous, and hinder understanding. That's the topic of this section.

Below, I'm going to illustrate with an example. I've condensed a sequence of equations where a triangle is being solved using both the Law of Cosines and the Law of Sines.

After I point out the ‘technical inaccuracies’ with the following sequence, I take a look at potential remedies. I will argue that, in my opinion, this first sequence is the best display of the solution . I welcome other opinions via the email on my homepage.

You don't need to know the math involved to follow the discussion on this page. But, for those who want to know, here 'tis:

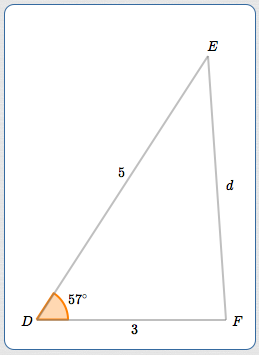
A triangle is given.

• Angle $\,D\,$ is opposite side $\,d\,.$
• Angle $\,E\,$ is opposite side $\,e\,.$
• Angle $\,F\,$ is opposite side $\,f\,.$

We're given: $\,D = 57^\circ\,,$ $\,e = 3\,,$ and $\,f = 5\,.$ The equations are numbered for ease of reference:

1.  $\,d^2 = 3^2 + 5^2 - 2\cdot 3\cdot 5\cdot\cos 57^\circ$

2.  $\,d^2 = 34 - 30\cos 57^\circ$
3.  $\,d \approx 4.202$
4.  $\,\displaystyle\frac{\sin 57^\circ}{4.202} = \frac{\sin E}{3}$

   (Although $\,4.202\,$ is displayed, you may want to use the full accuracy of your calculator for computation. See below.)

5.  $\,\displaystyle\sin E = \frac{3\sin 57^\circ}{4.202} \approx 0.5988$

   (Although $\,4.202\,$ is displayed, you may want to use the full accuracy of your calculator for computation. See below.)

6.  $\,E = \arcsin(0.5988) \approx 36.78^\circ$

   (Although $\,0.5988\,$ is displayed, you may want to use the full accuracy of your calculator for computation. See below.)

7.  $\,F = 180^\circ - 57^\circ - 36.78^\circ = 86.22^\circ$

   (Although $\,36.78\,$ is displayed, you may want to use the full accuracy of your calculator for computation. See below.)

Now, let me comment on this sequence of equations:

• (1), (2), and (3) are fine. No problems here.
• (4) is the first place an issue appears.

  Since an estimate for $\,d\,$ was used (from step 3), these two ratios, as written, aren't really equal. They're only approximately equal.

• The issue snowballs from there.

  Indeed, none of the equal signs in steps 5, 6, or 7 are truly correct, since each makes use of an approximation from an earlier step.

There is a convention being used in the display of this solution:

Let's verify that this convention has been applied in the sequence above:

• Step (3) was the first time $\,d\,$ was estimated, hence the use of  ‘$\,\approx\,$’.
• In step (4), no new approximation is being made, hence the use of  ‘$\,=\,$’.

• In the first part of step (5), there is no new approximation, hence the equal sign:

  $$\sin E = \frac{3\sin 57^\circ}{4.202}$$

  In the second part of step (5), there is a new approximation (for $\,\sin E\,$), hence the approximately equal sign:

  $$\frac{3\sin 57^\circ}{4.202} \approx 0.5988$$

• In the first part of step (6), there is no new approximation, hence the equal sign:

  $$E = \arcsin(0.5988)$$

  In the second part of step (6), there is a new approximation (for $\,E\,$), hence the approximately equal sign:

  $$\arcsin(0.5987) \approx 36.78^\circ$$

• In both parts of step (7), there are no new approximation errors being introduced.

  The first  ‘$\,=\,$’ sign uses a prior approximation.

  The second  ‘$\,=\,$’ sign is exact arithmetic.

Exploring Options for Remedying the Inaccuracy

One way to remedy the situation is to state an approximation, but then display only the exact value (using variable names) in future steps .

It's still important to state approximations, since you should be using common sense and checking for reasonableness of calculations at every step.

Potential Remedy #1 with Comments

1.  $\,d^2 = 3^2 + 5^2 - 2\cdot 3\cdot 5\cdot\cos 57^\circ$
2.  $\,d^2 = 34 - 30\cos 57^\circ$
3.  $\,d \approx 4.202$
4.  $\,\displaystyle\frac{\sin 57^\circ}{d} = \frac{\sin E}{3}$
5.  $\,\displaystyle\sin E = \frac{3\sin 57^\circ}{d} \approx 0.5987$

   (Note: Using more decimal places for $\,d\,$ gives a slightly more accurate value for the sine. Compare with $\,0.5988\,$ above.)

6.  $\,E = \arcsin(\sin E) \approx 36.78^\circ$
7.  $\,F = 180^\circ - 57^\circ - E \approx 86.22^\circ$

This approach has both advantages and disadvantages.

If you have a calculator that offers named memory locations (or can easily call up prior results), then—regardless of how you display your solution— you may want to use the full accuracy of your calculator in computations. This minimizes errors due to decimal approximations.

For example, here's a good calculator technique for finding $\,d\,.$ (Exact keystrokes differ from calculator to calculator.)

• To estimate $\,d^2\,$:

  Key in  3^2 + 5^2 - 2*3*5*cos(57)  (making sure you're in degree mode).

• Press  ENTER  to get a decimal approximation for $\,d^2\,.$
• Use the square root key to get a decimal approximation for $\,d\,.$
• Store the result in memory location $\,d\,.$

Then—whenever you need $\,d\,$—call it from memory. This minimizes errors introduced by decimal approximations. By writing $\,d\,$ instead of the approximate value  ‘$\,4.202\,$’  in step (4), it is both a strictly correct use of  ‘$\,=\,$’, and a reminder to you to use the stored value.

When you're working with lots of variables, however, you might lose track of which one(s) are already computed and stored in memory. A possible solution is to change the variable name to $\,d_{\text{stored}}\,$ (or $\,d_s\,$ for short), and use this as step (4):

Oops—but then we're back to the original problem. The number stored in the calculator likely isn't exactly $\,d\,,$ it's just a (much better) decimal approximation. Again, to be strictly correct, we'd need to say ‘$\,\approx\,$’ here.

One thing we lose in this ‘remedy’ is the ability to glance at an equation and know what has already been computed, and what still needs to be computed.

For example, a quick glance at  $\frac{\sin 57^\circ}{4.202} = \frac{\sin E}{3}$  reveals that $\,E\,$ is what needs to be computed.

However, a quick glance at  $\frac{\sin 57^\circ}{d} = \frac{\sin E}{3}\,,$ out of context, leaves one wondering if it's $\,d\,$ or $\,E\,$ we're seeking at this step.

My experience is that students follow calculations more easily when estimated values appear in the sequence. For a purist, though, this is a good solution display that encourages good calculator techniques.

Potential Remedy #2 with Comments

I think most educators will agree that if we insist on the following display, we'll unnecessarily scare many students away from math.

This one substitutes in the exact formulas for computed values all along the way:

1.  $\,d^2 = 3^2 + 5^2 - 2\cdot 3\cdot 5\cdot\cos 57^\circ$
2.  $\,d^2 = 34 - 30\cos 57^\circ$
3.  $\,d = \sqrt{34 - 30\cos 57^\circ}$
4.  $\,d \approx 4.202$
5.  $\,\displaystyle \frac{\sin 57^\circ}{d} = \frac{\sin 57^\circ}{\sqrt{34 - 30\cos 57^\circ}} = \frac{\sin E}{3}$
6.  $\,\displaystyle\sin E = \frac{3\sin 57^\circ}{\sqrt{34 - 30\cos 57^\circ}} \approx 0.5987$
7.  $\,\displaystyle E = \arcsin\left(\frac{3\sin 57^\circ}{\sqrt{34 - 30\cos 57^\circ}}\right) \approx 36.78^\circ$
8.   And the final computation: $$ \begin{align} F &= 180^\circ - 57^\circ - E\cr &=\ 180^\circ - 57^\circ - \arcsin\left(\frac{3\sin 57^\circ}{\sqrt{34 - 30\cos 57^\circ}}\right)\cr &\approx\ 86.22^\circ \end{align} $$

It's just scary looking. (But, every ‘$\,=\,$’ is strictly correct.)

Potential Remedy #3 with Comments

Another potential remedy is to use ‘$\,\approx\,$’ for everything that is truly an approximation. In this case, pretty much everything after the first occurrence of an approximation gets ‘$\,\approx\,$’:

1.  $\,d^2 = 3^2 + 5^2 - 2\cdot 3\cdot 5\cdot\cos 57^\circ$
2.  $\,d^2 = 34 - 30\cos 57^\circ$
3.  $\,d \approx 4.202$
4.  $\,\displaystyle\frac{\sin 57^\circ}{4.202} \approx \frac{\sin E}{3}$
5.  $\,\displaystyle\sin E \approx \frac{3\sin 57^\circ}{4.202} \approx 0.5988$
6.  $\,E \approx \arcsin(0.5988) \approx 36.78^\circ$
7.  $\,F \approx 180^\circ - 57^\circ - 36.78^\circ = 86.22^\circ$

I don't like this at all. It makes it ‘sound like’ (say) the Law of Sines only sort of works.

Potential Remedy #4 with Comments

One final potential remedy is to use an ellipsis ‘$\,\ldots\,$’ to indicate missing digits of a number.

In this case, no ‘approximately equal to’ signs are needed, but the trade-off is a lot of ‘dots’! Additionally, the display of  ‘$\,(36.78...)^\circ\,$’  is a bit kludgy.

1.  $\,d^2 = 3^2 + 5^2 - 2\cdot 3\cdot 5\cdot\cos 57^\circ$
2.  $\,d^2 = 34 - 30\cos 57^\circ$
3.  $\,d = 4.202...$
4.  $\,\displaystyle\frac{\sin 57^\circ}{4.202...} = \frac{\sin E}{3}$
5.  $\,\displaystyle\sin E = \frac{3\sin 57^\circ}{4.202...} = 0.5988...$
6.  $\,E = \arcsin(0.5988...) = (36.78...)^\circ$
7.  $\,F = 180^\circ - 57^\circ - (36.78...)^\circ = (86.22...)^\circ$

This approach could then add in uses of  ‘$\,\approx\,$’  to show rounding, e.g. ‘$\,d = 4.202... \approx 4.2\,$’.

It's just an awful lot of writing. Again—too much writing makes the math look harder than it really is.

Conclusion

In this author's humble opinion, the first sequence presented is best for most of our students and most of our teachers.

Some teachers may insist on students using the full accuracy of their calculators at each step, which is fine. Even in these cases, I don't think most teachers want their students to actually show (say) $\,4.202478905\,$ in their work (eeeeek).

In most problems, the decreased accuracy from failing to use all available decimal places (as opposed to a reasonable number of decimal places) usually doesn't prevent a teacher (or student) from recognizing a correct answer.