Introduction to Puncture Points (Holes)

Rational functions can exhibit puncture points (also called ‘holes’).

As you'll learn in Calculus, puncture points are an example of a ‘removable discontinuity’.

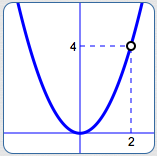
Here's the idea.

The function $\,\displaystyle R(x) := \frac{x^3-2x^2}{x-2}\,$ certainly looks like a typical rational function.

Upon closer inspection, though, we see that there's an extra factor of $\,1\,$ in the formula:

$$ \begin{align} \cssId{s6}{\frac{x^3 - 2x^2}{x - 2}}\ &\cssId{s7}{=\ \frac{x^2(x-2)}{x-2}}\cr\cr &\cssId{s8}{=\ x^2\cdot\frac{x-2}{x-2}} \end{align} $$

Therefore, $\,\displaystyle R(x) = \frac{x^3-2x^2}{x-2}\,$ has exactly the same outputs as the much simpler function, $\,P(x) := x^2\,,$ except that the function $\,R\,$ isn't defined when $\,x = 2\,.$

The graphs of both $\,P\,$ and $\,R\,$ are shown below—the puncture point (hole) in $\,R\,$ is caused by that extra factor of $\,1\,.$

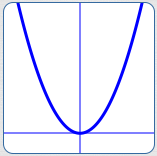
$P(x) = x^2$ the graph of P(x) = x^2

$$ \cssId{s13}{R(x)} \cssId{s14}{= \frac{x^3 - 2x^2}{x-2}} \cssId{s15}{= x^2\cdot\frac{x-2}{x-2}} $$ the graph of x^2, except with an extra factor of (x-2)/(x-2)

Puncture points are studied in more detail in a future section.