Logarithmic Functions: Review and Additional Properties (Part 2)

(This page is Part 2. Click here for Part 1.)

Going from Logarithmic Form to Exponential Form

Going from logarithmic form  ‘$\,\log_a y = x\,$’  to the equivalent exponential form  ‘$\,y = a^x\,$’  is easy! Start with the base ‘$\,a\,$’, circle counterclockwise to $\,x\,,$ and then to $\,y\,$:

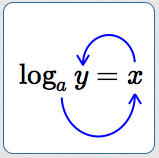
This circular motion actually gives  ‘$\,a^x = y\,$’. Then, write it again from right-to-left to get ‘$\,y = a^x\,$’ !

Going from Exponential Form to Logarithmic Form

Here's a thought process to go from exponential form  ‘$\,y = a^x\,$’   to the equivalent logarithmic form  ‘$\,\log_a y = x\,$’:

• We want a logarithmic form, so start by writing:  $\,\color{red}{\log}$
• The base of the logarithm is the same as the base of the exponential function, so add in the base:  $\,\color{red}{\log_a}$

• A logarithm is an exponent! The word ‘is’ translates as ‘$\,=\,$’.

  The only exponent in  ‘$\,y = a^x\,$’  is $\,x\,.$

  Leaving a space for the input, add in ‘$\,= x\,$’: $$\color{red}{\log_a\ \ \ = x}$$

• There's only one variable left in  ‘$\,y = a^x\,$’ , and only one place to put it!

  Finish by putting in the ‘$\,y\,$’ : $$\color{red}{\log_a y= x}$$

Domain/Range Considerations for Logarithmic and Exponential Functions

Let $\,a \gt 0\,,$ $\,a \ne 1\,.$ These are the allowable bases for logarithmic and exponential functions.

For exponential functions, $\,y = a^x\,$:

• the domain is the set of all real numbers
• the range is the set of positive real numbers

For logarithmic functions, $\,y = \log_a x\,$:

• the domain is the set of positive real numbers
• the range is the set of all real numbers

Observe that:

• the domain of $\,y = a^x\,$ is the range of $\,y = \log_a x\,$
• the range of $\,y = a^x\,$ is the domain of $\,y = \log_a x\,$

The input/output sets for inverses are switched! The input set for one is the output set for the other. The output set for one is the input set for the other.

Two Important Views of Logarithms

Now, you should be comfortable with both important views of logarithms:

• A Logarithm Is An Exponent:  What is $\,\log_a x\,$?

  It is the power (the exponent) that ‘$\,a\,$’ must be raised to, in order to get $\,x\,.$

• Logarithms ‘Undo’ Exponents:  If the exponential function with base $\,a\,$ takes input $\,x\,$ to output $\,y\,,$ then what function takes $\,y\,$ back to $\,x\,$?

  Answer: the logarithmic function with base $\,a\,$

Solving Inequalities Involving Logarithmic Functions

Equivalences (1), (2), and (3) (from Part 1) can be used to solve certain types of mathematical sentences involving logarithms, as illustrated in the following examples.

IMPORTANT: Whenever you have an expression of the form ‘$\,\log_a (\text{stuff})\,$’, the ‘stuff ’ must be positive!

Example 1

SOLVE:

This is an inequality of the form

where the base of the logarithm, $\,b\,,$ is $\,2\,.$

Notice that the logarithmic functions on both sides use the same base.

In this example, the base is greater than one, so we'll use equivalence $(1)$:

SOLUTION:

Since logarithms only act on positive numbers, we must also have:

Putting everything together:

The solution set of this inequality is:

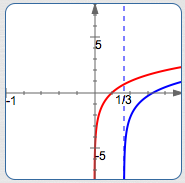
Blue curve:  $y = \log_2 (3x - 1)$

Red curve:  $y = \log_2 (5x)$

The blue curve is only defined for $\,x \gt \frac 13\,.$

The blue curve lies below the red curve everywhere that it is defined.

Head up to wolframalpha.com and type in:

log_2 (3x -1) < log_2 (5x)

Voila!

Example 2

SOLVE:

This is an inequality that can be easily transformed to

where the base of the logarithm, $\,b\,,$ is $\,0.3\,.$ Notice that the logarithm functions use the same base.

In this example, the base is between zero and one, so we'll use equivalence $(2)$:

Compare the solution below to what you get at wolframalpha.com:

log_(0.3) (7) - log_(0.3) (1 - 6x) > 0

SOLUTION:

Here are the reasons for each step:

• Original inequality
• Addition property for inequalities
• Equivalence $(2)$—inequality symbol changes direction; inputs to logs must be positive
• Addition property for inequalities
• Multiplication property for inequalities

• How can a number be both less than $\,-1\,$ and less than $\,\frac 16\,$ at the same time?

  Answer: By being less than $\,-1\,$!

Notice in the third step that the inequality symbol changed direction, since equivalence $(2)$ is being used.

Example 3

SOLVE:

Here's a screenshot from wolframalpha.com:

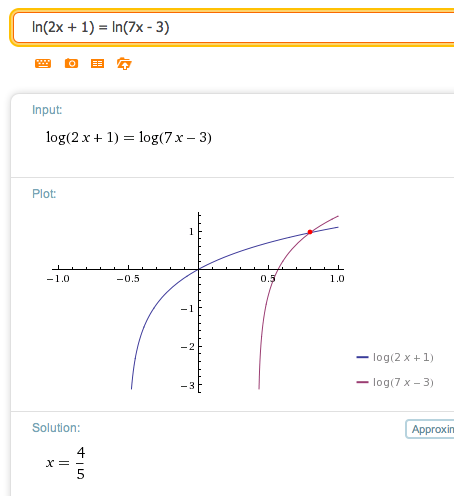
Writing a list of equivalent mathematical sentences: