Composition of Functions
See this earlier lesson for a thorough introduction to function composition.
Make sure you can do all the exercises there before moving on to this page.
This current lesson adds information and exercises concerning the domain of a composite function.
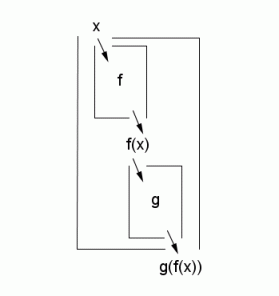
The function $\,g\circ f\ $:
$\,f\,$ is ‘closest to’ the input, and acts first;
$\,g\,$ acts second
The domain of $\,g\circ f\,$ is the set of inputs $\,x\,$ with two properties:
- $\,f\,$ must know how to act on $\,x\,.$ That is, $\,x\in\text{dom}(f)\,.$
- $\,g\,$ must know how to act on $\,f(x)\,.$ That is, $\,f(x)\in\text{dom}(g)\,.$
Thus:
$$ \begin{align} &\cssId{s18}{\text{dom}(g\circ f)}\cr &\quad \cssId{s19}{= \{x\ |\ x\in\text{dom}(f)\ \ \text{and}\ \ f(x)\in\text{dom}(g)\}} \end{align} $$Full-body virtual reality! Read about my family's first experiences with the Omni One at this page I wrote up. (At the bottom of the linked page, there are hilarious videos of our First Steps...)
Want to say hello? Sign my guestbook!
Example
This example is contrived to give practice with the domain of a composite function.
PROBLEM: Suppose that $\,f\,$ is the ‘add $\,3\,$’ function with a restricted domain:
$$\cssId{s27}{\text{dom}(f) = [0,2]}$$Thus, $\,f\,$ only knows how to act on the numbers $\,0\le x\le 2\,.$
Suppose that $\,g\,$ is the ‘subtract $\,5\,$’ function with a restricted domain:
$$ \cssId{s30}{\text{dom}(g) = [4,6]} $$Find the domains of both $\,g\circ f\,$ and $\,f\circ g\,.$
SOLUTION: We have:
$f(x) = x+3$ with $\text{dom}(f) = [0,2]$
and
$g(x) = x-5\,$ with $\text{dom}(g) = [4,6]$
Firstly, observe that the following sentences are equivalent:
$$ \begin{gather} \cssId{s38}{f(x)\in \text{dom}(g)}\cr\cr \cssId{s39}{x+3\in [4,6]}\cr\cr \cssId{s40}{4\le x+3 \le 6}\cr\cr \cssId{s41}{1\le x\le 3}\cr\cr \cssId{s42}{x\in [1,3]} \end{gather} $$Then,
$$ \begin{align} &\cssId{s44}{\text{dom}(g\circ f)}\cr\cr &\quad\cssId{s45}{= \{x\ |\ x\in\text{dom}(f)\ \ \text{and}\ \ f(x)\in\text{dom}(g)\}}\cr\cr &\quad\cssId{s46}{= \{x\ |\ x\in [0,2]\ \ \text{and}\ \ x\in[1,3]\}}\cr\cr &\quad\cssId{s47}{= \{x\ |\ x\in ([0,2]\cap[1,3])\}}\cr\cr &\quad\cssId{s48}{= \{x\ |\ x\in [1,2]\}}\cr\cr &\quad\cssId{s49}{= [1,2]} \end{align} $$Similarly (and a bit more compactly):
$$ \begin{align} &\cssId{s51}{\text{dom}(f\circ g)}\cr\cr &\quad\cssId{s52}{= \{x\ |\ x\in\text{dom}(g)\ \ \text{and}\ \ g(x)\in\text{dom}(f)\}}\cr\cr &\quad\cssId{s53}{= \{x\ |\ x\in [4,6]\ \ \text{and}\ \ x-5\in[0,2]\}}\cr\cr &\quad\cssId{s54}{= \{x\ |\ x\in [4,6]\ \ \text{and}\ \ x\in[5,7]\}}\cr\cr &\quad\cssId{s55}{= [5,6]} \end{align} $$
Concept Practice
- Choose a specific problem type, or click ‘New problem’ for a random question.
- Think about your answer.
- Click ‘Check your answer’ to check!