Addition and Subtraction Formulas for Sine and Cosine
Note: In the audio read-through—for simplicity/brevity—I sometimes read ‘$\,\sin x\,$’ as just ‘sine ex’ instead of ‘sine of ex’.
This section explores four trigonometric identities:
- Addition Formula for Cosine: $$\cssId{s3}{\cos(a\color{blue}{\bf +}b) = \cos a\ \cos b \color{red}{\bf -} \sin a\ \sin b}$$
- Subtraction Formula for Cosine: $$\cssId{s5}{\cos(a\color{red}{\bf -}b) = \cos a\ \cos b \color{blue}{\bf +} \sin a\ \sin b}$$
- Addition Formula for Sine: $$\cssId{s7}{\sin(a\color{blue}{\bf +}b) = \sin a\ \cos b \color{blue}{\bf +} \cos a\ \sin b}$$
- Subtraction Formula for Sine: $$\cssId{s9}{\sin(a\color{red}{\bf -}b) = \sin a\ \cos b \color{red}{\bf -} \cos a\ \sin b}$$
Sum and Difference Formulas for Sine and Cosine
The boxes below include: Variety of Names, the formulas (‘For all real numbers $\,a\,$ and $\,b\,$’), and Shorthand Notations.
Cosine Formulas
Variety of Names
- Addition Formula for Cosine
- Sum Formula for Cosine
- Cosine Addition Formula
- Cosine Sum Formula
For all real numbers $\,a\,$ and $\,b\,$:
$$\cssId{s18}{\cos(a\color{blue}{\bf +}b) = \cos a\ \cos b \color{red}{\bf -} \sin a\ \sin b}$$Variety of Names
- Subtraction Formula for Cosine
- Difference Formula for Cosine
- Cosine Subtraction Formula
- Cosine Difference Formula
For all real numbers $\,a\,$ and $\,b\,$:
$$\cssId{s23}{\cos(a\color{red}{\bf -}b) = \cos a\ \cos b \color{blue}{\bf +} \sin a\ \sin b}$$Shorthand Notations
These two formulas are often presented with this shorthand:
$$ \cssId{s25}{\cos(a\color{orange}{\boldsymbol\pm} b) = \cos a\ \cos b \ \color{purple}{\boldsymbol\mp}\ \sin a\ \sin b} $$Note that:
- ‘$\,\color{orange}{\boldsymbol\pm}\,$’ is read as ‘plus or minus’
- ‘$\,\color{purple}{\boldsymbol\mp}\,$’ is read as ‘minus or plus’
- The plus sign (top left) in $\,\color{orange}{\boldsymbol\pm}\,$ goes with the minus sign (top right) in $\,\color{purple}{\boldsymbol\mp}\,.$
- The minus sign (bottom left) in $\,\color{orange}{\boldsymbol\pm}\,$ goes with the plus sign (bottom right) in $\,\color{purple}{\boldsymbol\mp}\,.$
Sine Formulas
Variety of Names
- Addition Formula for Sine
- Sum Formula for Sine
- Sine Addition Formula
- Sine Sum Formula
For all real numbers $\,a\,$ and $\,b\,$:
$$\cssId{s35}{\sin(a\color{blue}{\bf +}b) = \sin a\ \cos b \color{blue}{\bf +} \cos a\ \sin b}$$Variety of Names
- Subtraction Formula for Sine
- Difference Formula for Sine
- Sine Subtraction Formula
- Sine Difference Formula
For all real numbers $\,a\,$ and $\,b\,$:
$$\cssId{s40}{\sin(a\color{red}{\bf -}b) = \sin a\ \cos b \color{red}{\bf -} \cos a\ \sin b}$$Shorthand Notations
These two formulas are often presented with this shorthand:
$$\cssId{s42}{\sin(a\pm b) = \sin a\ \cos b \ \pm\ \cos a\ \sin b}$$Note that:
- ‘$\,\pm\,$’ is read as ‘plus or minus’
- The plus sign (top left) in $\,\pm\,$ goes with the plus sign (top right) in $\,\pm\,.$
- The minus sign (bottom left) in $\,\pm\,$ goes with the minus sign (bottom right) in $\,\pm\,.$
Memory Device
For the sine sum/difference formulas:
- When there's a plus sign on the left, there's a plus sign on the right.
- When there's a minus sign on the left, there's a minus sign on the right.
Thus, Sine is the Same. (For the cosine formula, they're different.)
Verbalizing/Recalling the Sum Formulas
For the Cosine
The sum formula for the cosine gives the cosine of a sum in terms of the sine and cosine of the addends:
Here's a way to recall, from memory, the formula for $\,\cos(a + b)\,$:
- First write the pattern: $$\cssId{s67}{\cos\,\cos\ \ \ \ \ \ \sin\,\sin}$$
- Recall: Sine is the Same; cosine is different. Thus, the plus sign in $\,\cos(a \color{red}{\boldsymbol +} b)\,$ gets changed to a minus sign: $$\cssId{s70}{\cos\,\cos\ \color{red}{\boldsymbol -}\ \sin\,\sin}$$
- Put the addends in place (twice), in the same order as they appear in $\,\cos(a+b)\,$: $$\cssId{s72}{\cos a\,\cos b\ \color{red}{-}\ \sin a\,\sin b}$$
For the Sine
The sum formula for the sine gives the sine of a sum in terms of the sine and cosine of the addends:
Here's a way to recall, from memory, the formula for $\,\sin(a + b)\,$:
-
First write the pattern: $$\sin\,\cos\ \ \ \ \ \ \cos\,\sin$$
- Recall: Sine is the Same. Thus, the plus sign in $\,\sin(a \color{red}{\boldsymbol +} b)\,$ remains a plus sign: $$\cssId{s88}{\sin\,\cos\ \color{red}{\boldsymbol +}\ \cos\,\sin}$$
- Put the addends in place (twice), in the same order as they appear in $\,\sin(a+b)\,$: $$\cssId{s90}{\sin a\,\cos b\ \color{red}{+}\ \cos a\,\sin b}$$
There are similar verbalizations and memory recall methods for the difference formulas.
Example: Using the Sum Formulas
Let's use some special angles for an example. You know that $\cos 90^\circ = 0\,$ and $\sin 90^\circ = 1\,.$ Do the sum formulas give these results?
$$ \begin{align} &\cssId{s97}{\cos 90^\circ = \cos (30^\circ + 60^\circ)}\cr\cr &\quad\cssId{s98}{\overset{\text{?}}{=}}\ \cssId{s99}{\cos 30^\circ\cos 60^\circ - \sin 30^\circ\sin 60^\circ}\cr\cr &\quad\cssId{s100}{\, =\ \frac {\sqrt 3}2\cdot \frac{1}{2} - \frac{1}{2} \cdot \frac {\sqrt 3}2 = 0\ \text{Yep!}} \end{align} $$$$ \begin{align} &\cssId{s101}{\sin 90^\circ = \sin (30^\circ + 60^\circ)}\cr\cr &\quad\cssId{s102}{\overset{\text{?}}{=}}\ \cssId{s103}{\sin 30^\circ\cos 60^\circ + \cos 30^\circ\sin 60^\circ}\cr\cr &\quad\cssId{s104}{\, = \frac{1}{2}\cdot\frac{1}{2} + \frac{\sqrt 3}{2}\cdot\frac {\sqrt 3}2 = \frac 14 + \frac 34 = 1\ \text{Yep!}} \end{align} $$
You should do similar examples (say, writing $\,30^\circ = 90^\circ - 60^\circ\,$) to give some confidence in the difference formulas.
Proving the Sum Formulas for Sine and Cosine
An identity is a mathematical sentence that is always true. The sum formulas given above can't be proved using the simple strategies outlined in Verifying Trigonometric Identities. They require some cleverness!
When I was talking about these identities one day, my genius husband (Ray) drew a sketch which gives both formulas. The sketch is shown below, together with step-by-step details of how to get the sum formulas from the sketch. I love it!
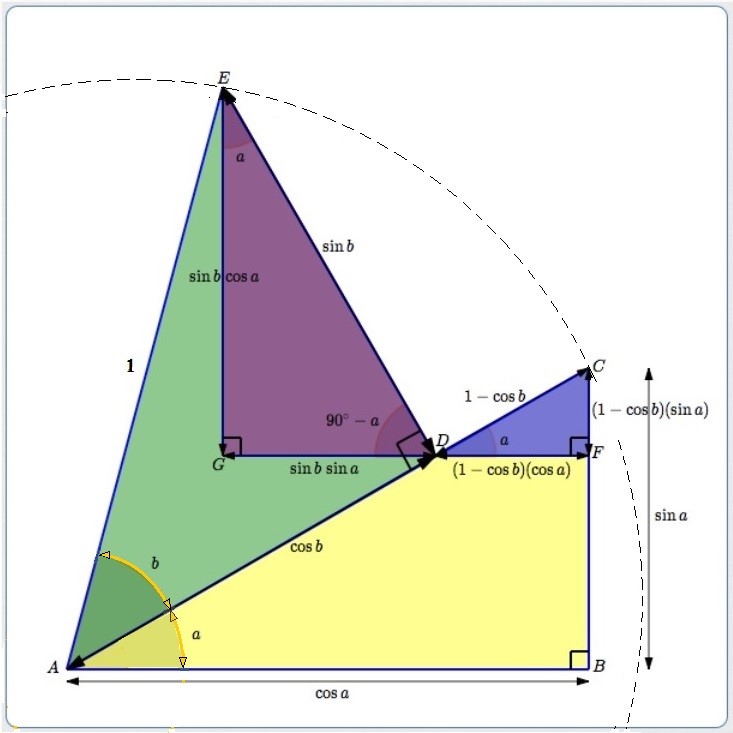
Put the origin at point $\,A\,.$ Assume both $\,a\,$ and $\,b\,$ are measured in degrees.
Start with right triangle $\,\triangle ABC\,$ (mostly yellow). It has acute angle $\,a\,$ and hypotenuse of length $\,1\,.$ Thus:
- Bottom leg: $\,\cos a$
- Side leg: $\,\sin a$
Stack a right triangle $\,\triangle ADE\,$ (mostly green) on the hypotenuse of the yellow triangle. It has acute angle $\,b\,$ and hypotenuse of length $\,1\,.$ Thus:
- Bottom leg: $\,\cos b$
- Side leg: $\,\sin b$
The blue right triangle:
- Since $\,\overline{DF}\, ||\, \overline{AB}\,,$ $\,\angle CDF = a\,$
- Hypotenuse: $\,1 - \cos b\,$
- Bottom leg: $\,(1-\cos b)(\cos a)\,$
- Side leg: $\,(1-\cos b)(\sin a)\,$
The purple right triangle:
- By vertical angles, $\,\angle ADG = a\,$
- Thus: $\,\angle EDG = 90^\circ - a\,$
- Thus: $\,\angle DEG = a\,$
- Hypotenuse: $\,\sin b\,$
- Bottom leg: $\,\sin b\,\sin a$
- Side leg: $\,\sin b\,\cos a$
With all side lengths in place, the sum formulas are now easy:
$$
\begin{align}
&\cssId{s146}{\cos(a+b)}\cr\cr
&\quad\cssId{s147}{\ =\ \cos a - (1-\cos b)(\cos a) - \sin b\,\sin a}\cr
&\qquad\quad\cssId{s148}{\text{($x$-value of point $\,E\,$) }}\cr\cr
&\quad\cssId{s149}{\ =\ \cos a - \cos a + \cos b\,\cos a - \sin b\,\sin a}\cr
&\qquad\quad\cssId{s150}{\text{(distributive law)}}\cr\cr
&\quad\cssId{s151}{\ =\ \cos a\,\cos b - \sin a\,\sin b}\cr
&\qquad\quad\cssId{s152}{\text{(cancel; commutative property of multiplication)}}
\end{align}
$$
$$
\begin{align}
&\cssId{s153}{\sin(a+b)}\cr\cr
&\quad\cssId{s154}{=\ \sin a - (1-\cos b)(\sin a) + \sin b\,\cos a} \cr
&\qquad\quad\cssId{s155}{\text{($y$-value of point $\,E\,$) }}\cr\cr
&\quad\cssId{s156}{\ =\ \sin a - \sin a + \cos b\,\sin a + \sin b\,\cos a}\cr
&\qquad\quad\cssId{s157}{\text{(distributive law)}}\cr\cr
&\quad\cssId{s158}{\ =\ \sin a\,\cos b + \cos a\,\sin b}\cr
&\qquad\quad\cssId{s159}{\text{(cancel; commutative property of multiplication)}}
\end{align}
$$
For the sketch given here, all angles are acute:
$$ \begin{gather} \cssId{s161}{0 \lt a \lt 90^\circ}\cr \cssId{s162}{0 \lt b \lt 90^\circ}\cr \cssId{s163}{\,0 \lt a+b \lt 90^\circ} \end{gather} $$This proof can be extended for other angles. Or, a proof for all real numbers can be found in standard texts.
Proving the Difference Formulas for Sine and Cosine
Since subtraction is a special kind of addition, the difference formulas follow easily from the sum formulas.
$$ \begin{align} &\cssId{s168}{\cos(a-b)}\cr\cr &\qquad\cssId{s169}{= \cos (a + (-b))}\cr &\qquad\quad\cssId{s170}{\text{(to subtract $b$, add the opposite)}}\cr\cr &\qquad\cssId{s171}{= \cos(a)\,\cos(-b) - \sin(a)\,\sin(-b)}\cr &\qquad\quad\cssId{s172}{\text{(sum formula for cosine)}}\cr\cr &\qquad\cssId{s173}{= \cos(a)\,\cos(b) - \sin(a)\bigl(-\sin(b)\bigr)}\cr &\qquad\quad\cssId{s174}{\text{(cosine is even; sine is odd)}}\cr\cr &\qquad\cssId{s175}{= \cos a\,\cos b + \sin a\,\sin b}\cr &\qquad\quad\cssId{s176}{\text{(simplify)}} \end{align} $$$$ \begin{align} &\cssId{s177}{\sin(a-b)}\cr\cr &\qquad\cssId{s178}{= \sin (a + (-b))}\cr &\qquad\quad\cssId{s179}{\text{(to subtract $b$, add the opposite)}}\cr\cr &\qquad\cssId{s180}{= \sin(a)\,\cos(-b) + \cos(a)\,\sin(-b)}\cr &\qquad\quad\cssId{s181}{\text{(sum formula for sine)}}\cr\cr &\qquad\cssId{s182}{= \sin(a)\,\cos(b) + \cos(a)\bigl(-\sin(b)\bigr)}\cr &\qquad\quad\cssId{s183}{\text{(cosine is even; sine is odd)}}\cr\cr &\qquad\cssId{s184}{= \sin a\,\cos b - \cos a\,\sin b}\cr &\qquad\quad\cssId{s185}{\text{(simplify)}} \end{align} $$