Increasing and Decreasing Functions

DEFINITIONS increasing/decreasing functions

A function $\,f\,$ increases on an interval $\,I\,$

if and only if

whenever $\,a \lt b\,$ in $\,I\,,$ $\,f(a) \lt f(b)\,.$

A function $\,f\,$ decreases on an interval $\,I\,$

if and only if

whenever $\,a \lt b\,$ in $\,I\,,$ $\,f(a) \gt f(b)\,.$

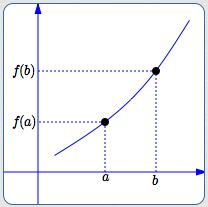an increasing function

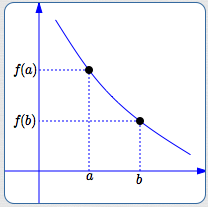a decreasing function

Roughly:

Increasing means going strictly uphill, as you move from left to right on a graph.
Decreasing means going strictly downhill, as you move from left to right on a graph.