Is there an ‘SSA’ Congruence Theorem? No!

You may want to review: Triangle Congruence

So far, we have four theorems that give conditions under which two triangles are guaranteed to be congruent:

• Knowing two angles in a triangle uniquely determines the third angle, and hence the shape of the triangle. Then, knowing the length of one side specifies the size of the triangle. These observations lead to the ASA (an included side) and AAS (also called SAA; a non-included side) congruence theorems.
• Imagine two boards of fixed length, attached with a hinge. Opening the hinge a specified amount uniquely determines a triangle. This leads to the SAS congruence theorem.
• As long as the third side has length less than the sum of the hinged sides (and also isn't too short), then the hinge can be opened just enough to attach the third board. This observation leads to the SSS congruence theorem.

A natural question then arises: is there an ‘SSA’ congruence theorem? That is, if you know two sides and a non-included angle, is a unique triangle determined?

The discussion below shows that the general answer is ‘no’. However, there are special cases where, with a bit more information, a unique triangle is determined.

Exploring the ‘SSA’ Condition For Triangles

Pick a point on a dashed line (see diagrams below) and attach a side of a specified length at a specified angle. A second side will be attached to the first. Observe that this configuration gives two sides and a non-included angle.

Depending on the length of the second side relative to the first, different things can happen, as discussed below.

Second Side Too Short—No Triangle

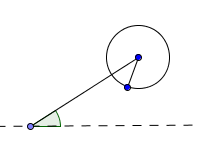
If the second side is too short, then it will just wave around in the air. No matter what angle it is attached at, it will never be long enough to reach the dashed line and form a triangle.

In this situation, there does not exist a triangle with the given two sides and non-included angle.

Second Side Just the Right Length—A Unique Right Triangle

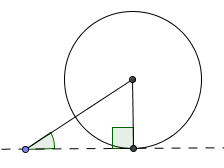
If the second side is just the right length , then it will hit the dashed line at a single point. In this case, a unique right triangle is determined. One of the known sides is the hypotenuse; the other side is one of the legs.

With a slightly different approach, suppose you know the hypotenuse and one of the legs in a right triangle. Using the Pythagorean Theorem, the third side is then uniquely determined.

These observations give the following HL (Hypotenuse Leg) Congruence Theorem, which is a special case of an ‘SSA’ congruence, for right triangles:

Second Side a Bit Too Long—Two Different Triangles

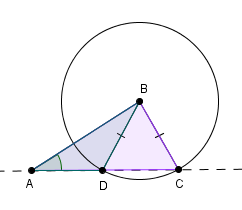
This case is the reason there is no ‘SSA’ congruence theorem. If you make the second side even longer, then two different triangles can be formed.

That is, $\,\Delta ABD\,$ and $\,\Delta ABC\,$ both satisfy the ‘SSA’ condition: two sides and a non-included angle are the same. However, they are not congruent.

There's a common memory device to avoid this tempting ‘SSA’ situation; it comes from noticing that reading ‘SSA’ backwards gives the name of a donkey. Don't be a ‘backwards SSA’ and think that there's an ‘SSA’ congruence!

Second Side Same as the First—A Unique Isosceles Triangle

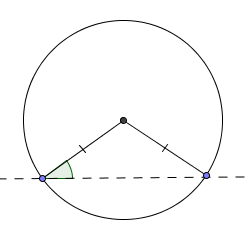
If the length of the second side is exactly the same as the first side, then a (unique) isosceles triangle is formed.

Recall that an isosceles triangle has at least two sides of equal length.

Second Side Longer than the First Side—A Unique Triangle

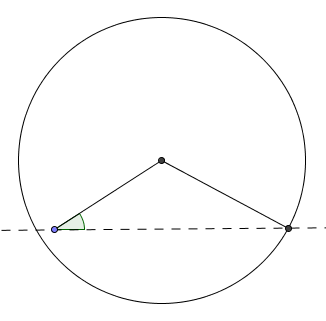
To complete the argument, make the second side longer than the first side. Again, a unique triangle is formed that has the specified angle.