• Jump right to the exercises!
• You may also want to review basic properties of logarithmic functions:
  Introduction to Logarithmic Functions

Most of your experience thus far has likely been with functions where the
base is a variable, and the exponent is a constant, like these:

• [beautiful math coming... please be patient] $\,y=x=x^1\,$   (the identity function)
• $\,y=x^2\,$   (the squaring function)
• $\,y=x^3\,$   (the cubing function)
• $\,y=\sqrt{x}=x^{1/2}\,$   (the square root function)
• [beautiful math coming... please be patient] $\,y=\frac{1}{x}=x^{-1}\,$   (the reciprocal function)

Functions with a variable base and a constant exponent are called power functions.
Switch the role of variable and constant and you get an entirely new family of functions,
called exponential functions, which are the subject of this section.
For example, these are all exponential functions:

• $y=2^x$
• [beautiful math coming... please be patient] $y={(\frac{1}{2})}^x$
• $\,y={\text{e}}^x$

The precise definition follows:

If you hear the phrase ‘the exponential function’ (meaning only one)
then the function being referred to is [beautiful math coming... please be patient] $\,y={\text{e}}^x=\exp(x)\,$.

Some mathematicians (this author included) tend to call more general functions
with a constant base and variable in the exponent exponential functions;
say, $\ y={\text{e}}^{2x-3}\ $ or [beautiful math coming... please be patient] $\ y=-7\cdot 3^{5-x}\,$.
However, for the purposes of this section,
the phrase exponential function refers only to functions of the form $\,y=b^x\,$.

Why must the base of an exponential function be positive?
For negative numbers, there are problems for many values of $\,x\,$;
for example, [beautiful math coming... please be patient] $\,(-4)^{1/2} = \sqrt{-4}\,$ is not a real number.

Why can't the base be $\,1\,$ or $\,0\,$?
The base can't be $\,1\,$, because [beautiful math coming... please be patient] $\,1^x \ \overset{\text{always}}{=}\ 1\,$, so the function $\,1^x\,$ is a constant function.
There is a similar problem with zero as the base.

There are two basic shapes to the graphs of exponential functions,
depending on whether the base is greater than $\,1\,$, or between $\,0\,$ and $\,1\,$:

[beautiful math coming... please be patient] $\,y=b^x\,$   for   $\,b\gt 1\,$	$\,y=b^x\,$   for   $\,0\lt b\lt 1\,$
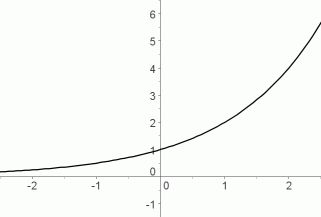
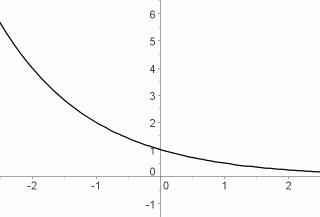
increasing functions; also called growth functions	decreasing functions; also called decay functions

PROPERTIES OF THE GRAPH for $\,b\gt 1\,$ An increasing function has the following property: as you walk along the graph, going from left to right, you are always going UPHILL. The following are equivalent for a function [beautiful math coming... please be patient] $\,f(x)=b^x\,$: $f\,$ is an increasing function $b\gt 1\,$ For increasing exponential functions: as $\,x\rightarrow \infty \,$, [beautiful math coming... please be patient] $\,y\rightarrow \infty \,$ Read this aloud as:   as $\,x\,$ goes to infinity, $\,y\,$ goes to infinity as $\,x\rightarrow -\infty \,$, $\,y\rightarrow 0\,$ Read this aloud as:   as $\,x\,$ goes to negative infinity, $\,y\,$ approaches zero It is important to note that increasing exponential functions increase VERY quickly. For example, suppose you are walking along the graph of [beautiful math coming... please be patient] $\,y={\text{e}}^x\,$, moving from left to right. By the time $\,x\,$ is $\,7\,$, the outputs are already greater than $\,1000\,$. Even more impressive is this fact: as you pass through the point that has $\,y$-value $\,1000\,$, the slope of the tangent line is also $\,1000\,$, so the outputs are changing $\,1000\,$ times faster than the inputs at this point! It would feel like you are climbing a vertical cliff (see below)! (Now, repeat this paragraph with the number $\,1000\,$ replaced by ANY large number of your choosing!)

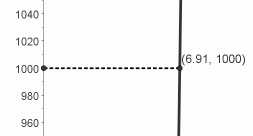
[beautiful math coming... please be patient] $y = b^x\,$   for   $\,b \gt 1$ increasing functions as $\,x\rightarrow \infty \,$, $\,y\rightarrow \infty \,$ as $\,x\rightarrow -\infty \,$, $\,y\rightarrow 0\,$

PROPERTIES OF THE GRAPH for $\,0\lt b\lt 1\,$ A decreasing function has the following property: as you walk along the graph, going from left to right, you are always going DOWNHILL. The following are equivalent for a function [beautiful math coming... please be patient] $\,f(x)=b^x\,$: $\,f\,$ is a decreasing function $\,b\,$ is between $\,0\,$ and $\,1\,$ For decreasing exponential functions: as [beautiful math coming... please be patient] $\,x\rightarrow \infty \,$, $\,y\rightarrow 0\,$ Read this aloud as:   as $\,x\,$ goes to infinity, $\,y\,$ approaches zero as $\,x\rightarrow -\infty \,$, $\,y\rightarrow \infty \,$ Read this aloud as:   as $\,x\,$ goes to negative infinity, $\,y\,$ goes to infinity

[beautiful math coming... please be patient] $y = b^x\,$   for   $\,0 \lt b \lt 1$ decreasing functions as $\,x\rightarrow \infty \,$, $\,y\rightarrow 0 \,$ as $\,x\rightarrow -\infty \,$, $\,y\rightarrow \infty\,$

Let [beautiful math coming... please be patient] $\,f(x)=b^x\,$, where $\,b\,$ is a positive number not equal to $\,1\,$.
For all (allowable) bases $\,b\,$, exponential functions share the following properties:

• the domain is the set of all real numbers:   [beautiful math coming... please be patient] $\,\text{dom}(f)=\mathbb{R}\,$
• the range is the set of all positive real numbers:   $\,\text{ran}(f)=(0,\infty)\,$
• the graph crosses the $\,y$-axis at $\,y = 1$
• the graph passes both the vertical and horizontal line tests

THE DOMAIN IS THE SET OF ALL REAL NUMBERS: [beautiful math coming... please be patient] $\text{dom}(f) = \mathbb{R}$ If the graph of an exponential function is ‘collapsed’ into the $\,x$-axis, sending each point on the graph to its $\,x$-value, then the entire $\,x$-axis will be hit. Exponential functions know how to act on all real number inputs. For basic information on the domain and range of a function, you may want to review: Domain and Range of a Function

THE RANGE IS THE SET OF ALL POSITIVE REAL NUMBERS: [beautiful math coming... please be patient] $\text{ran}(f)=(0,\infty )$ If the graph of an exponential function is ‘collapsed’ into the $\,y$-axis, sending each point on the graph to its $\,y$-value, then all positive $\,y\,$-values will be hit. Outputs from exponential functions are always positive. Having trouble understanding the expression ‘$\,(0,\infty)\,$’? Then, you may want to review Interval and List Notation.

THE GRAPH CROSSES THE $\,y\,$-AXIS AT $\,y=1\,$ For allowable values of $\,b\,$,   [beautiful math coming... please be patient] $\,b^0 \ \overset{\text{always}}{\ \ =\ \ }\ 1\,$. So, when the input is $\,0\,$ to the function $\,y=b^x\,$, the output is $\,1\,$. Thus, the point $\,(0,1)\,$ lies on the graph of every exponential function.

Imagine a vertical line sweeping through a graph, checking each allowable $\,x$-value:
if it never hits the graph at more than one point, then the graph is said to pass the vertical line test.
All functions pass the vertical line test, since the function property is that each input has exactly one output.

passes the vertical line test: each $\,x$-value has only one $\,y$-value all functions pass the vertical line test

fails the vertical line test: there exists an $\,x$-value that has more than one $\,y$-value

Imagine a horizontal line sweeping through a graph, checking each allowable $\,y$-value:
if it never hits the graph at more than one point, then the graph is said to pass the horizontal line test.
Some functions pass the horizontal line test, and some do not.

passes the horizontal line test: each $\,y$-value has only one $\,x$-value all exponential functions pass the horizontal line test

fails the horizontal line test: there exists a $\,y$-value that has more than one $\,x$-value some functions fail the horizontal line test

Thus, exponential functions have a wonderful property:
each input has exactly one output (passes the vertical line test), and
each output has exactly one input (passes the horizontal line test).

For such functions, you can think of the inputs/outputs as being connected with strings:
pick up any input, and follow its ‘string’ to the unique corresponding output;
pick up any output, and follow its ‘string’ to the unique corresponding input.
That is, there is a one-to-one correspondence between the inputs and outputs.
Functions with this property are called one-to-one functions.

You can use GeoGebra to explore exponential functions, by clicking on the link below.
(Please be patient. It may take a few minutes for GeoGebra to load.)