 Equations of Circles
Equations of Circles
For this lesson, you need to understand the technique of: Completing the Square
While the important technique of completing the square is on your fingertips, it's a good time to discuss the equations of circles.
Suppose that a circle has center $\,(h,k)\,$ and radius $\,r\,$ (where $\,r \ge 0\,$). Let $\,(x,y)\,$ be a typical point on this circle. Refer to the diagram below.
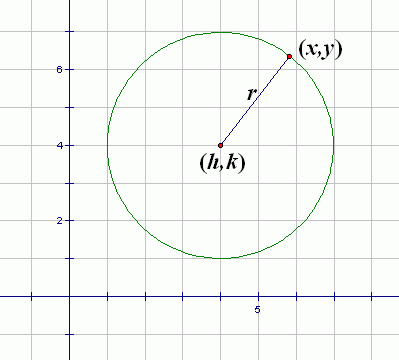
The distance from $\,(x,y)\,$ to $\,(h,k)\,$ must equal $\,r\,$:
$$\cssId{s8}{\sqrt{(x-h)^2 + (y-k)^2} =r}$$Recall from The Distance Formula that the distance between points $\,(x_1,y_1)\,$ and $\,(x_2,y_2)\,$ is given by the formula: $$\cssId{s10}{\sqrt{ {(x_2-x_1)}^2 + {(y_2-y_1)}^2}}$$
$$(x-h)^2 + (y-k)^2 = r^2$$
To eliminate the bothersome square root, square both sides. Thus, we have:
For example, consider the equation: $$\cssId{s20} { { (x-3)}^2 + {(y+5)}^2 = 15}$$ What does the graph of this equation look like? That is, what does the set of all points $\,(x,y)\,$ that makes this equation true look like?
To answer, rename $\,5\,$ as $\,-(-5)\,$ and $\,15\,$ as $\,{(\sqrt{15})}^2\,,$ and compare with the standard form of a circle:
$$ \begin{alignat}{4} &{(x-3)}^2 &&\ +\ &&{(y+5)}^2 &&\ =\ &15\cr\cr &{(x-3)}^2 &&\ +\ &&{(y-(-5))}^2 &&\ =\ &(\sqrt{15})^2\cr\cr &{(x-h)}^2 &&\ +\ &&{(y-k)}^2 &&\ =\ &r^2 \end{alignat} $$
Thus, $\,h = 3\,,$ $\,k = -5\,,$ and $\,r = \sqrt{15}\,.$ The equation graphs as the circle with center $\,(h,k) = (3,-5)\,$ and radius $\,r = \sqrt{15}\,.$
Students sometimes like to think of it this way:
-
The $x$-value of the center of the circle is the value of $\,x\,$ that makes $\,x-h\,$ equal to zero.
In our example, what makes $\,x-3\,$ equal to zero? Answer: $\,3\,$
-
The $y$-value of the center of the circle is the value of $\,y\,$ that makes $\,y-k\,$ equal to zero.
In our example, what makes $\,y+5\,$ equal to zero? Answer: $\,-5\,$
-
The radius of the circle is the square root of the right-hand side of the equation.
In our example, what is the square root of $\,15\,$? Answer: $\,\sqrt{15}\,$
You can use WolframAlpha to find the radius, center, and graph of a circle. Just type in (say):
radius and center of (x - 3)^2 + (y + 5)^2 = 15
Voila!
How to Recognize the Equation of a Circle
Unfortunately, circles aren't always given to you in this nice standard form. Sometimes they're given to you all multiplied out. In this situation, you should still be able to recognize that you're dealing with a circle, and you should be able to put it in standard form.
For example, if you multiply out $$(x-3)^2 + (y+5)^2 = 15$$ here's what you get:
$$ \cssId{s47}{x^2 - 6x + 9 + y^2 + 10y + 25 = 15} $$Using the Addition and Multiplication Properties of Equality, it can look even different, say: $$ \cssId{s49}{12x - 2x^2 -20y = 38 + 2y^2} $$
If the equation were originally given to you in this form, you should still be able to recognize it as a circle! (For fun, type this last equation into WolframAlpha to convince yourself that we're still dealing with the same circle.)
The process of identifying circles is actually quite easy, as discussed next.
Multiplying out the left-hand side of the equation $${(x-h)}^2+{(y-k)}^2=r^2$$ gives:
$$ \cssId{s54}{x^2 - 2xh + h^2 + y^2 - 2ky + k^2 = r^2} $$The key observation is that there are only five types of terms: $\,x^2\,,$ $\,y^2\,,$ $\,x\,,$ $\,y\,,$ and constant. And, when the $\,x^2\,$ and $\,y^2\,$ terms are on the same side of the equation, then they will have the same coefficient.
These observations lead to the following way to recognize circles:
Let $\,b\,,$ $\,c\,,$ and $\,d\,$ be real numbers, and let $\,a\,$ be a nonzero real number.
Equations of the form $$ \cssId{s64}{ax^2 + ay^2+bx+cy=d} $$ graph as circles.
You must have both $\,x^2\,$ and $\,y^2\,$ terms, and they must have the same coefficient, when they are on the same side of the equation.
You are allowed (but not required) to have $\,x\,,$ $\,y\,,$ and constant terms. You may not have any other term types.
It is possible to end up with a circle with radius zero, sometimes called a ‘point’ circle, like $\,x^2+y^2 = 0\,.$ The only solution to this equation is $\,(0,0)\,.$
It is also possible to end up with an ‘imaginary’ circle, like $\,x^2 + y^2 = -1\,.$ In this case, there are no real numbers $\,x\,$ and $\,y\,$ that make the equation true.
The following example illustrates the process of recognizing the equation of a circle and putting it in standard form so that it can be easily graphed.
Example
Question: Identify the graph of $\,3x^2 - 5x - 7 = 1 - 3y^2\,.$ If possible, graph the equation.
Solution: There are both $\,x^2\,$ and $\,y^2\,$ term types, and they have the same coefficient when they are on the same side of the equation. The other terms in this equation are $\,x\,$ and constant terms, which are allowable term types for a circle. Therefore, this is the equation of a circle.
Put it in standard form as follows:
On both sides, add $$\bigl(\frac{-5/3}{2}\bigr)^2 = \bigl(-\,\frac{5}{3\cdot 2}\bigr)^2 = \frac{25}{36}\ ,$$
which is the appropriate number to complete the square.
Thus, this is the circle with center $\,(\frac{5}{6},0)\,$ and radius $\,\frac{11}{6}\,.$ Check this result with WolframAlpha! (You may need to click the ‘Properties’ tab to get some of the desired information.)
Once you know the center and radius of a circle, there are always four points that are easy to plot. Start at the center, and move up/down left/right by the amount of the radius.
Another way to gain confidence in your work is to check at least one of these four easy points in the original equation. Let's check the point $\,(\frac{5}{6},\frac{11}{6})\,$:
$$ \begin{gather} \cssId{s107}{3x^2 - 5x - 7 = 1 - 3y^2}\cr\cr \cssId{s108}{3\left(\frac{5}{6}\right)^2 - 5\left(\frac{5}{6}\right) - 7 \ \ \overset{\text{? }}{=}\ \ 1 - 3\left(\frac{11}{6}\right)^2}\cr\cr \cssId{s109}{-\frac{109}{12} = -\frac{109}{12}\qquad \text{Yes!}} \end{gather} $$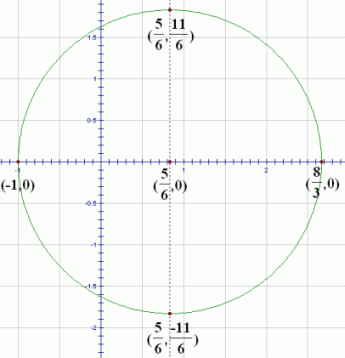
To finish up, you may want to jump up to wolframalpha.com and type in, say:
equation of circle with center (3,-4) and radius square root of 2
Pretty amazing!