 Rounding Decimals to a Specified Number of Places
Rounding Decimals to a Specified Number of Places
When you're solving a problem where an approximation suffices for the answer, the most commonly-requested approximation looks something like this:
“Please round to $\,2\,$ decimal places”
or equivalently,
“Please round to the hundredths place”
The purpose of this section is to discuss the concept and the technique of rounding.
Let's start with an example. Suppose you're asked to round $\,x = 2.73845\,$ to two decimal places. The number $\,x = 2.73845\,$ lies between $\,2.73\,$ and $\,2.74\,$ on the number line. Indeed, it lies just about here:
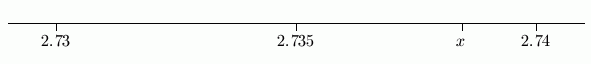
If we're rounding to two decimal places, then the two ‘candidates’ for the desired approximation are $\,2.73\,$ and $\,2.74\,.$ Which candidate is $\,x\,$ closest to?
Answer: $\,2.74\,$
So we say:
“$\,2.73845\,,$ rounded to $\,2\,$ decimal places, is $\,2.74\,$”
or equivalently,
“$\,2.73845\,,$ rounded to the hundredths place, is $\,2.74\,$”
You could now be asked the follow-up question:
“Did you round up, or round down?”
When the candidate to the right of the original number is chosen, we say that we are rounding up, because we're moving ‘up’ (to the right) on the number line to get the approximation.
When the candidate to the left of the original number is chosen, we say that we are rounding down, because we're moving ‘down’ (to the left) on the number line to get the approximation.
To ‘round to $\,n\,$ decimal places’ means to choose the closest neighbor that uses exactly $\,n\,$ decimal places.
When the two candidates are equidistant, the normal convention is to round UP; that is, choose the candidate on the right.
Note: If there's concern about an upward bias to the data, then you can use a no-bias rounding convention.
Efficient Technique for Rounding
The ideas illustrated in the previous example can be efficiently implemented as follows.
| ROUNDING TO $\,\,n\,\,$ DECIMAL PLACES | |
| GENERAL PROCEDURE |
EXAMPLE: Round $\,2.73845\,$ to $\,2\,$ decimal places. |
|
STEP 1: (rounding digit) Go to the digit in the $\,n^{\text{th}}\,$ decimal place. This is called the rounding digit. |
Because we're rounding to $\,n = 2\,$ decimal places, we want the digit in the second decimal place: $$2.7\underline{3}845$$ The rounding digit is $\,3\,.$ |
|
STEP 2: (decider digit) Look at the next digit to the right. This is called the decider digit. It is used to decide whether to round up or down (next step). |
What digit is to the right of the
$\,3\,$?
$$2.7\underline{3}{\bf8}45$$
Answer: $\,8\,$
The decider digit is $\,8\,.$ |
|
STEP 3: (rounding UP or DOWN) If the decider digit is less than $\,5\,,$ then round DOWN: the rounding digit remains the same, and all the digits to the right are dropped. If the decider digit is $\,5\,$ or more, then round UP: the rounding digit increases by $\,1\,,$ and all the digits to the right are dropped. If the rounding digit is $\,9\,$ and you're rounding up, this is a special case. See the next step! |
Our decider digit is
$\,8\,,$ which is more than $\,5\,.$
We need to round UP. The rounding digit increases by $\,1\,$ (from $\,3\,$ to $\,4\,$); all digits to the right are dropped. So, $\,2.73845\,$ rounds to $\,2.74\,.$ |
|
SPECIAL CASE: ROUNDING DIGIT IS $\,9\,,$ ROUNDING UP If the rounding digit is $\,9\,$ and you're rounding up, then the rounding digit becomes a $\,0\,$ (which you keep), and the next digit to the left increases by $\,1\,.$ You may need to apply this rule more than once. Whenever a $\,9\,$ must be increased by $\,1\,,$ then the $\,9\,$ becomes a $\,0\,$ (which you keep), and the next digit to the left increases by $\,1\,.$ |
NEW EXAMPLE:
Round
$\,2.79845\,$ to $\,2\,$ decimal places.
The rounding digit is $\,9\,.$ The decider digit is $\,8\,,$ so we round UP. The $\,9\,$ becomes a $\,0\,$ (which we keep); the digit to the left increases by $\,1\,$ (from $\,7\,$ to $\,8\,$). So, $\,2.79845\,$ rounds to $\,2.80\,.$ Good way to think of this: the ‘$\,79\,$’ in $\,2.\underline{79}845\,$ becomes an ‘$\,80\,$’. |
Examples
(The decider digit is $\,1\,$; round down.)
(The decider digit is $\,9\,$; round up.) Notice that you must include the $\,0\,$ in the thousandths place.
(The decider digit is $\,9\,$; round up.) Notice that you must include the two trailing zeros.
(The decider digit is $\,2\,$; round down.)
(The decider digit is $\,8\,$; round up.) Notice that you must include all the trailing zeros.
Careful!
When you are asked to round a number to $\,n\,$ decimal places, then your answer must have $\,n\,$ decimal places, even if there are zeros in those positions.
More Examples
Answer: $\,0.927$
If the decimal is less than $\,1\,,$ then it is good style to put a zero in the ones place.
In the web exercise below, you must put the zero in the ones place to be recognized as correct.
Answer: $\,3.0000$
If you round to $\,4\,$ decimal places, then your answer must have $\,4\,$ decimal places, even if there are zeros in those positions.