Practice with Radicals
The concept of doing something and then ‘undoing’ it is very important in mathematics. Here are some examples:
Take a number. Add $\,5\,$ to it. How can you get back to the original number? Answer: subtract $\,5\,.$ That is, addition is ‘undone’ with subtraction.
Take a number. Multiply it by $\,7\,.$ How can you get back to the original number? Answer: divide by $\,7\,.$ That is, multiplication is ‘undone’ with division.
In this section, we address the issue of ‘undoing’ powers, like this:
Cube it—that is, raise it to the third power.
How can you get back to the original number?
Questions like this lead us to an understanding of a mathematical expression called a radical.
Undoing Odd Powers
Let's revisit the scenario in the previous paragraph:
Take the number $\,2\,.$ Cube it, to get $\,8\,.$ Now, think about the thought process needed to get back to the original number. You must think: What number, when cubed, gives $\,8\,$? The answer is of course $\,2\,.$
One more time. Take the number $\,-2\,.$ Cube it, to get $\,-8\,.$ Ask the question: What number, when cubed, gives $\,-8\,$? The answer is $\,-2\,.$
Notice that there is only one number which, when cubed, gives $\,8\,.$ This unique number is denoted by the symbol $\displaystyle\,\root 3\of{8}\,$ and is called the cube root of $\,8\,.$
Also, there is only one number which, when cubed, gives $\,-8\,.$ This unique number is denoted by the symbol $\displaystyle\,\root 3\of{-8}\,$ and is called the cube root of $\,-8\,.$
The ‘cube root’ process undoes the ‘cube’ process. Roots undo powers. The idea is stated more formally below.
Let $\,x\,$ be any real number.
The number $\displaystyle\,\root 3\of{x}\,,$ read as the cube root of $\,x\,,$ is defined as follows:
$\displaystyle\,\root 3\of{x}\,$ is the unique number which, when cubed, equals $\,x\,.$
Don't ever lose sight of the fact that numbers have lots of different names. Both $\,2\,$ and $\,\root 3\of{8}\,$ are names for the same number. Thus, the sentence ‘$\,\root 3\of{8} = 2\,$’ is true.
There's a good visual check for problems like this. As shown below, make a circle, checking that your answer ($\,2\,$), raised to the third power, does indeed equal $\,8\,.$
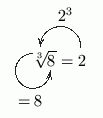
Here's a more general definition for odd roots:
Let $\,x\,$ be any real number, and let $n\in\{3,5,7,\ldots\}\,.$
The number $\displaystyle\,\root n\of{x}\,,$ read as the $n^{\text{th}}\,$ root of $\,x\,,$ is defined as follows:
$\displaystyle\,\root n\of{x}\,$ is the unique number which, when raised to the $\,n\,$ power, equals $\,x\,.$
‘Undoing’ Even Powers
Next, we'll try to ‘undo’ even powers, and will see that two problems emerge. Before beginning, recall that $\,2^2 = 4\,$ and $\,(-2)^2 = 4\,.$ That is, there are two numbers (both $\,2\,$ and $\,-2\,$) which, when squared, give $\,4\,.$
So, suppose I tell you that I'm thinking of a number. When I square this number, I get $\,4\,.$ Can you tell me which number I'm thinking of? No—I could be thinking of the number $\,2\,,$ or the number $\,-2\,.$ This is the first problem with even roots.
The question “What number, when squared, gives $\,4\,$?” is flawed, because there is not a unique number with this property.
We must instead ask a different question in order to get a unique answer: “What nonnegative number, when squared, gives $\,4\,$?” Then, the answer is $\,2\,.$
The symbol $\,\sqrt{4}\,$ is read as ‘the square root of $\,4\,$’ and represents the nonnegative number which, when squared, gives $\,4\,.$
Next, suppose you are asked to find $\,\sqrt{-4}\,.$ Is there any real number which, when squared, gives $\,-4\,$? A positive number, when squared, is positive. A negative number, when squared, is again positive. Thus, no real number exists which has the property that squaring it gives $\,-4\,$ as the result.
This is the second problem. You can't take the square root of negative numbers.
Thus, we are led to the precise definition of the square root, which is characteristic of the behavior of all even roots:
Let $\,x \ge 0\,.$
The number $\displaystyle\,\sqrt{x}\,,$ read as the square root of $\,x\,,$ is defined as follows:
$\displaystyle\,\sqrt{x}\,$ is the nonnegative number which, when squared, equals $\,x\,.$
Here's the generalization of the definition to cover all even roots:
Let $\,x \ge 0\,,$ and let $n\in\{2, 4,6,\ldots\}\,.$
The number $\displaystyle\,\root n\of{x}\,,$ read as the $n^{\text{th}}\,$ root of $\,x\,,$ is defined as follows:
$\displaystyle\,\root n\of{x}\,$ is the unique nonnegative number which, when raised to the $\,n\,$ power, equals $\,x\,.$
For $\,n = 2\,,$ the special notation $\,\sqrt{x}\,\,$ (instead of $\,\root 2\of{x}\,$) is used, and is read as the square root of $\,x\,.$
Radicals
All even and odd roots go by a common name:
The term radical refers to a particular name for a number. Both $\,\sqrt{4}\,$ and $\,2\,$ are names for the same number: $\,\sqrt{4}\,$ is called a radical, but $\,2\,$ isn't. You must see the root symbol ‘$\,\sqrt{\,\,}\,$’ for an expression to be called a radical.
Whenever you're presented with a radical, you must first decide if you're dealing with an odd root or an even root.
Odd roots are defined for all real numbers, but even roots are only defined for nonnegative numbers.
Odd roots can give nonnegative or negative answers, but even roots only give nonnegative answers, when they exist.
After more than 25 years of developing this site, I am now seeking a successor organization to acquire OneMathematicalCat.org and carry it forward into the future. Learn more about this opportunity ➜
Want to say hello? Sign my guestbook!
Examples
Check: $\,6\,$ is nonnegative, and $\,6^2 = 36\,$
Check: $\,2^3 = 8$
Check: $\,1\,$ is nonnegative, and $\,1^4 = 1\,$
Check: $\,(-1)^5 = -1$
Input ‘nd’ for ‘not defined’.
Check: $\,0^7 = 0$
Check: $\,\frac{1}{4}\,$ is nonnegative, and $\,(\frac{1}{4})^2 = \frac{1}{16}\,$
Check: $\,(-\frac{1}{2})^3 = -\frac{1}{8}$
Practice
Input ‘nd’ for ‘not defined’.