Practice with Order of Operations

The order that operations are to be performed (when not clearly identified) is summarized with the following memory device:

Please Excuse My Dear Aunt Sally
(PEMDAS)

Do things inside Parentheses first (using PEMDAS, if needed, inside the parentheses).
Then do all Exponents, in order as they occur, going from left to right.
Then do all Multiplications/Divisions (they have equal weight) in order as they occur, going from left to right.
Finally, do all Additions/Subtractions (they have equal weight) in order as they occur, going from left to right.

In September 2017, this problem was floating around the web:

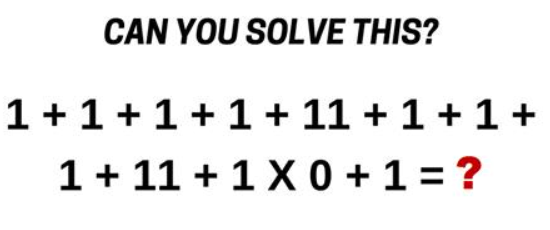
PEMDAS from web

Here's the solution, with correct order of operations:

$$ \begin{align} &\cssId{s19}{1 + 1 + 1 + 1 + 11 + 1 + 1 + 1 + 11 + 1\times 0 + 1} \cr\cr &\quad\cssId{s20}{= 1 + 1 + 1 + 1 + 11 + 1 + 1 + 1 + 11 + (1\times 0) + 1}\cr &\quad\quad\cssId{s21}{\text{(the multiplication gets done first)}} \cr\cr &\quad\cssId{s22}{= 1 + 1 + 1 + 1 + 11 + 1 + 1 + 1 + 11 + 0 + 1}\cr\cr &\quad\cssId{s23}{= 30} \end{align} $$

If this doesn't make sense to you, try the following mental exercise on a shorter (but similar) problem: $$\cssId{s25}{1 + 2 \times 0 + 3}$$

Replace each plus sign with an (equally-weak) person.
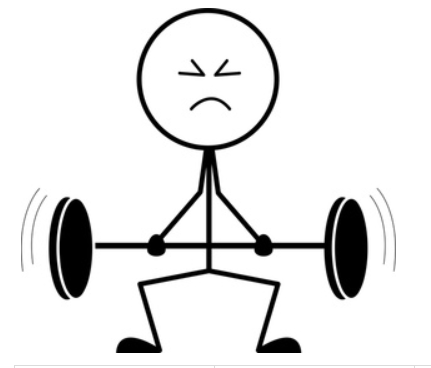
Replace the multiplication sign with a strong person. Why? Multiplication is ‘stronger than’ addition! And this makes perfectly good sense, since multiplication is ‘super-addition’. For example: $$\cssId{s31}{\,5\times 2 = 2 + 2 + 2 + 2 + 2}$$
The first (left-most) weak guy is trying to pull together the $\,1\,$ and the $\,2\,,$ to add them.
The middle (strong) guy is trying to pull together the $\,2\,$ and the $\,0\,,$ to multiply them.
The right-most weak guy is trying to pull together the $\,0\,$ and the $\,3\,,$ to add them.
Who wins? Clearly, the strong guy!

1 weak man 2 strong man 0 3

$$ \begin{align} &\cssId{s37}{1 + 2 \times 0 + 3}\cr &\qquad\cssId{s38}{=\ \ 1 + \overbrace{(2\times 0)}^{\text{strong guy wins}} + 3}\cr\cr &\qquad\cssId{s39}{=\ \ 1 + 0 + 3}\cr\cr &\qquad\cssId{s40}{=\ \ 4} \end{align} $$

More Examples

$ \begin{align} &\cssId{s42}{-1 + 3\times 5 - 2}\cr\cr &\qquad\cssId{s43}{= -1 + (3\times 5) - 2}\cr\cr &\qquad\cssId{s44}{= 12} \end{align} $

$ \begin{align} &\cssId{s45}{2 - 10\div 5 + 3}\cr\cr &\qquad\cssId{s46}{= 2 - \frac{10}{5} + 3}\cr\cr &\qquad\cssId{s47}{= 3} \end{align} $

Curious readers may want to explore the optional section: Laurel, Yanny, Cookies, Bananas, and Clocks

Practice

Feel free to use a pencil and scrap paper to work these problems. However, do not use your calculator!