Simplifying Basic Absolute Value Expressions

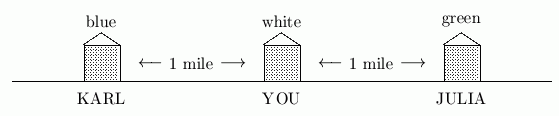
Suppose you live in the white house shown below. Julia lives in the green house to the right, and Karl lives in the blue house to the left.

Karl and Julia live in different places, but they both live the same distance from your home. To visit Julia, you walk one way. To visit Karl, you walk the other way.

Suppose you were asked the question: “Who lives one mile from you on this street?” You would respond by saying: “Well—two people. Julia lives one mile this way, and Karl lives one mile that way.”

Absolute Value as Distance From Zero

This section explores the idea of distance from home, under the guise of a mathematical concept called absolute value.

Now, think of home as being position $\,0\,$ on a number line. Instead of talking about distance from home, we'll talk about distance from zero. When you talk about distance from zero, it's critical to remember that you can walk away from $\,0\,$ in two directions: to the right, or to the left.

Suppose you're asked the question: “What numbers are three units from $\,0\,$ on a number line?” The number $\,3\,$ is three units from $\,0\,$; it is $\,3\,$ units to the right of $\,0\,.$ Also, the number $\,-3\,$ is three units from $\,0\,$; it is $\,3\,$ units to the left of $\,0\,.$

Opposites (like $\,3\,$ and $\,-3\,$) always have the same distance from $\,0\,$: one is to the right of zero, and one is to the left of zero.

The Notation $\,|x|\,$

The notation ‘$\,|x|\,$’ (the number $\,x\,$ inside vertical bars) is used to represent the distance between the number $\,x\,$ and $\,0\,.$ The notation ‘$\,|x|\,$’ is read as ‘the absolute value of $\,x\,$’. Whenever you see the vertical bars ‘$\,|\ \ |\,$’ your first thought should be distance from $\,0\,.$

The symbol $\,|3|\,$ (the absolute value of three) represents the distance between $\,3\,$ and $\,0\,.$ Thus, $\,|3| = 3\,,$ since the number $\,3\,$ is $\,3\,$ units from zero.

The symbol $\,|-3|\,$ (the absolute value of negative three) represents the distance between $\,-3\,$ and $\,0\,.$ Thus, $\,|-3| = |3|\,,$ since the number $\,-3\,$ is $\,3\,$ units from zero.

Notice that $\,|3|\,$ and $\,|-3|\,$ are both mathematical expressions—they are numbers.

Geometric Definition of Absolute Value

There are two common definitions of $\,|x|\,$: a geometric definition (which follows), and an algebraic definition. The algebraic definition is presented in a future section.

Absolute Value is Always Nonnegative

Whenever you report distance, you give a number that is greater than or equal to zero. (You would never say: “I live $\,-2\,$ miles from my Mom.”) Since $\,|x|\,$ reports a distance, it follows that $\,|x|\,$ is always greater than or equal to zero.

Recall that ‘nonnegative’ means ‘greater than or equal to zero’. Thus, $\,|x|\,$ is a nonnegative quantity. No matter what is inside the absolute value symbols, the resulting number is always nonnegative. Thus, $\,|\,\text{any stuff}\,|\,$ is always greater than or equal to zero, regardless of what the ‘stuff’ is.

Two Important Properties of Absolute Value

Here are two important properties of absolute value:

Minus Signs Inside Versus Outside Absolute Values

When working with absolute value expressions, you must pay attention to whether a minus sign is inside the absolute value or outside, because it makes a big difference!

Use the fact that $\,|x| = |-x|\,$ to deal with minus signs that are inside.

A minus sign outside an absolute value denotes multiplication by $\,-1\,.$ For example:

Here, you will practice simplifying expressions involving absolute value. Write all answers without absolute value symbols. Do not use a calculator for these problems.

Examples

Practice