Changing Decimals to Percents

Need some basic practice with decimals first? Changing Decimals to Fractions and Multiplying and Dividing Decimals by Powers of Ten

One use for decimals is in working with percents, which are commonplace in everyday life:

• the dress was on sale for $\,40\%\,$ off the original price;
• housing costs rose $\,5\%\,$ last year;
• there was a $\,150\%\,$ increase in telephone activity after the newspaper advertisement.

There are $\,100\,$ cents in a dollar. A century is $\,100\,$ years. The word  percent  means  per one hundred .

The symbol  $\%$  is used for percent. Whenever you see the symbol   $\%$ , you can trade it in for a factor of $\,\frac{1}{100}\,.$ Whenever you see a factor of $\,\frac{1}{100}\,,$ it can be traded in for a  $\%$  symbol. This simple idea is the key to success with percents:

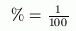
Indeed, the symbol  $\%$  even looks a bit like the fraction $\,\frac{1}{100}\,$; it has the two zeros and the division bar!

To change from a decimal to a percent, move the decimal point two places to the right and insert the percent symbol.

Examples

Here's the idea that makes this work:

Notice that the $\displaystyle\,\frac{1}{100}\,$ gets traded in for the percent symbol.

Practice