 Review of Circles (and Related Concepts)
Review of Circles (and Related Concepts)
Definition of Circle
By definition, a circle is the set of all points in a plane that are the same distance from a fixed point (called its center).
Notes:
Circle Determined By a Point and Nonnegative Real Number
Let $\,C := (h,k)\,$ be a point. Let $\,r\,$ be a nonnegative real number. Using set-builder notation:
$$ \begin{align} &\cssId{s13}{\text{The circle determined by $\,C\,$ and $\,r\,$}}\cr\cr &\quad \cssId{s14}{=\{\ (x,y)\ |\ \text{the distance from $\,(x,y)\,$ to $\,(h,k)\,$ is $\,r$ } \ \}} \cr\cr &\quad \cssId{s15}{= \{\ (x,y)\ |\ \sqrt{(x-h)^2 + (y-k)^2} = r\ \}}\cr\cr &\quad \cssId{s16}{= \{\ (x,y)\ |\ (x-h)^2 + (y-k)^2 = r^2\ \}} \end{align} $$Point Circle
If $\,r = 0\,,$ the circle degenerates to a single point—its center. In this case, it is called a ‘point circle’.
Interior of a Circle
The interior of the circle with center $\,(h,k)\,$ and radius $\,r\,$ is:
$$ \cssId{s20}{\{(x,y)\ |\ (x-h)^2 + (y-k)^2 \lt r^2 \,\}} $$A circle does not include its interior; it is the boundary (of the interior) only. In particular, a (non-point) circle does not include its center.
See Equations of Circles for more information.

A circle (in green) with center $\,C$
Radius of a Circle
Depending on context, radius can mean:
- the distance from the center to any point on the circle
- a line segment from the center to a point on the circle
Note that the length of a radius (as in 2) is the radius of the circle (as in 1).
The plural of ‘radius’ is either:
- ‘radii’ (pronounced ray-dee-eye)
- ‘radiuses’
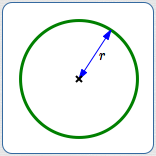
Radius ($\,r\,$) as a distance (a nonnegative number)
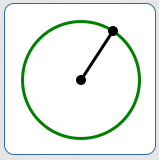
Radius as a line segment
Diameter of a Circle
Depending on context, diameter can mean:
- twice the radius (a nonnegative number)
- a line segment passing through the center of a circle, with both endpoints on the circle
Note that the length of a diameter (as in 2) is the diameter of the circle (as in 1).
In algebra, precalculus, calculus, and life (!) contexts, the words radius and diameter typically refer to numbers (distances).
In geometry contexts, the words radius and diameter often refer to line segments.
From context, it should always be clear whether the words radius and diameter refer to numbers (possibly with units) or line segments.
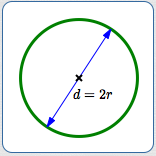
Diameter ($\,2r\,$) as a distance (a nonnegative number)
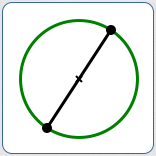
Diameter as a line segment
Circumference of a Circle
The circumference of a circle is the distance around the circle.
As discussed below:
$$ \cssId{s49}{\text{Circumference} = 2\pi r = \pi d\ ,} $$where $\,r\,$ is the radius and $\,d = 2r\,$ is the diameter.
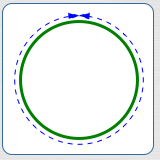
Circumference of a circle: the distance around the circle
The Irrational Number Pi
Compute with circles, and you're certain to run into the special number $\,\pi\ $:
Symbol Used for Pi
The symbol ‘$\,\pi\,$’ is a lowercase letter in the Greek alphabet. It is spelled ‘pi’ (no ‘e’ on the end). It is pronounced ‘pie’ (as in apple pie or cherry pie).
Hands-On Understanding of $\,\pi\,$
Grab any circular object (like a plate).
Measure its c i r c u m f e r e n c e and diameter. (Use a string or a flexible ruler.) Be sure to use the same units for both measurements.
Take the circumference and divide by the diameter—you'll get a number a bit more than $\,3\,$!
Repeat with a different circular object, then another (until bored).
Any differences in your calculations—as you use different size circles—are due only to measurement errors.
Definition of Pi
For circles, the ratio of circumference to diameter is always the same! This was known by Babylonians and Egyptians at least 4000 years ago.
By definition, $\,\pi\,$ is the ratio of circumference to diameter in a circle.
Leonhard Euler began the use of the symbol ‘$\,\pi\,$’ for this ratio in 1737.
$$ \cssId{s72}{\pi = \frac{\text{circumference}}{\text{diameter}}} $$The formula for the circumference of a circle follows immediately:
$$ \cssId{s74}{\text{circumference} = \pi(\text{diameter})} $$Pi is Irrational
The number $\,\pi\,$ is irrational (not rational). This means:
- It has no representation as a ratio of integers. A common rational approximation is $\,\pi\approx\frac{22}{7}\,.$
- It has an infinite, non-repeating decimal expansion. A common decimal approximation is $\,\pi\approx 3.14\,.$
- For more decimal places of pi, look below, or go to Wolfram|Alpha and type in ‘pi’.
Practical Interpretation of Pi
Keep in mind what all this is saying! In any circle, if you walk all the way around, you'll travel just over three times further than if you walk straight across (passing through the center) to the opposite side.

By definition, $\,\pi\,$ is the ratio of circumference to diameter in a circle:
$$ \cssId{s87}{\pi := \frac{\color{blue}{\text{circumference}}}{\color{red}{\text{diameter}}} \approx 3.14} $$Thus:
$$\cssId{s89}{\text{circumference} \approx (3.14)(\text{diameter})}$$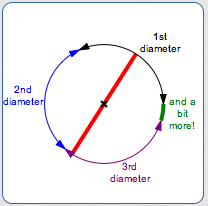
It takes just over $\,3\,$ diameters to go around the circle!
Pi is irrational, hence has an infinite, non-repeating decimal expansion.
$\pi\,$ is approximately:
3 . 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6
4 3 3 8 3 2 7 9 5 0 2 8 8 4 1 9 7 1 6 9 3 9 9
3 7 5 1 0 5 8 2 0 9 7 4 9 4 4 5 9 2 3 0 7 8 1
6 4 0 6 2 8 6 2 0 8 9 9 8 6 2 8 0 3 4 8 2 5 3
4 2 1 1 7 0 6 7 9 8 2 1 4 8 0 8 6 5 1 3 2 8 2
3 0 6 6 4 7 0 9 3 8 4 4 6 0 9 5 5 0 5 8 2 2 3
1 7 2 5 3 5 9 4 0 8 1 2 8 4 8 1 1 1 7 4 5 0 2
8 4 1 0 2 7 0 1 9 3 8 5 2 1 1 0 5 5 5 9 6 4 4
6 2 2 9 4 8 9 5 4 9 3 0 3 8 1 9 6 4 4 2 8 8 1
0 9 7 5 6 6 5 9 3 3 4 4 6 1 2 8 4 7 5 6 4 8 2
3 3 7 8 6 7 8 3 1 6 5 2 7 1 2 0 1 9 0 9 1 4 5
6 4 8 5 6 6 9 2 3 4 6 0 3 4 8 6 1 0 4 5 4 3 2
6 6 4 8 2 1 3 3 9 3 6 0 7 2 6 0 2 4 9 1 4 1 2
7 3 7 2 4 5 8 7 0 0 6 6 0 6 3 1 5 5 8 8 1 7 4
8 8 1 5 2 0 9 2 0 9 6 2 8 2 9 2 5 4 0 9 1 7 1
5 3 6 4 3 6 7 8 9 2 5 9 0 3 6 0 0 1 1 3 3 0 5
3 0 5 4 8 8 2 0 4 6 6 5 2 1 3 8 4 1 4 6 9 5 1
9 4 1 5 1 1 6 0 9 4 3 3 0 5 7 2 7 0 3 6 5 7 5
9 5 9 1 9 5 3 0 9 2 1 8 6 1 1 7 3 8 1 9 3 2 6
1 1 7 9 3 1 0 5 1 1 8 5 4 8 0 7 4 4 6 2 3 7 9
9 6 2 7 4 9 5 6 7 3 5 1 8 8 5 7 5 2 7 2 4 8 9
1 2 2 7 9 3 8 1 8 3 0 1 1 9 4 9 1 2 9 8 3 3 6
7 3 3 6 2 4
Central Angle of a Circle
By definition, a central angle in a circle is an angle formed at the center of a circle by two radii.
Notes on Central Angles
By convention, ‘central angle’ refers to the smaller of the two angles determined by two radii.
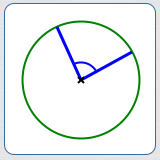
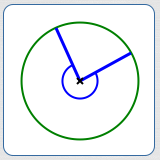
That is—unless otherwise requested—a central angle is between $\,0^\circ\,$ and $\,180^\circ\,.$ If you want the bigger central angle, ask for the ‘reflex central angle’.
The name ‘central angle’ is appropriate, since the vertex of a central angle is the center of a circle.
The sizes of angles ($\,\theta\,$) are often described using these words:
| The zero angle: | equal to zero | $\,\theta = 0^\circ\,$ |
| Acute: | strictly between $\,0^\circ\,$ and $\,90^\circ\,$ | $\,0^\circ \lt \theta \lt 90^\circ\,$ |
| Right: | equal to $\,90^\circ$ | $\theta = 90^\circ$ |
| Obtuse: | strictly between $\,90^\circ\,$ and $\,180^\circ\,$ | $\,90^\circ \lt \theta \lt 180^\circ\,$ |
| Straight: | equal to $\,180^\circ$ | $\theta = 180^\circ$ |
| Reflex: | strictly between $\,180^\circ\,$ and $\,360^\circ\,$ | $180^\circ \lt \theta \lt 360^\circ$ |

A central angle (the smaller angle determined by two radii)

A reflex central angle (the bigger angle determined by two radii)