Reading Information from the Graph of a Function

Suggested Review:  Graphs of Functions from the Algebra II curriculum

You must be able to read a wide variety of information from the graph of a function:

• Function values
• Function values on lines between two known points
• Domain of the function (using correct set notation)
• Range of the function (using correct set notation)
• Where the function increases/decreases/is constant
• Sets of inputs for which the output has specified properties

Example

The graph of a function $\,f\,$ is given below.

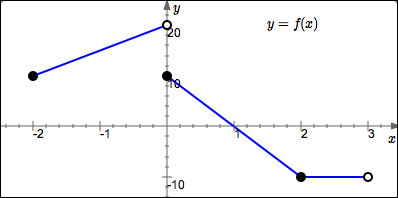
$f(0) = 10$

$f(1) = 0$

$f(2.03) = -10$

$\text{dom}(f) = [-2,3)$

$\text{ran}(f) = [-10,20)$

$f$ increases on $[-2,0)$

$f$ decreases on $[0,2]$

$f$ is constant on $[2,3)$

$\{x\ |\ f(x) = 10\} = \{-2,0\}$

$\{t\ |\ f(t) \gt 0\} = [-2,1)$

How can we tell this is the graph of a function?   It passes the vertical line test.