Graphs of Sine and Cosine

The graphs of the sine and cosine functions are shown below.

• Where do these graphs come from?
• Important characteristics of the graphs
• Two trigonometric identities

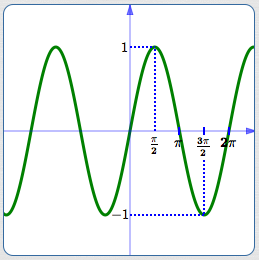
Graph of $\,y = \sin x$

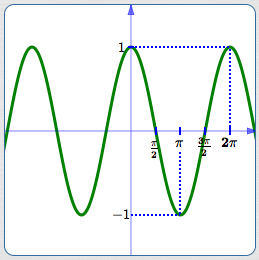
Graph of $\,y = \cos x$

Where Do These Graphs Come From?

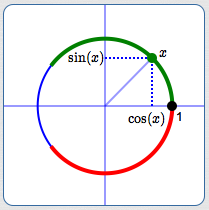
The sine function gives the $y$-values of points on the unit circle.

The cosine function gives the $x$-values of points on the unit circle.

Since the unit circle has radius $\,1\,,$ all its points have coordinates between $\,-1\,$ and $\,1\,.$ That's why both graphs (sine and cosine) are trapped between $\,y = -1\,$ and $\,y = 1\,.$

Visualizing the Graph of the Sine Function

Here's a way you can visualize the graph of the sine function:

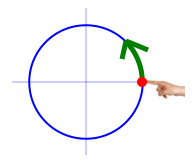
Put your finger at the point $\,(1,0)\,$ on the unit circle. Twirl it around the circle counter-clockwise (start UP). The sine function tracks your finger's up/down motions:

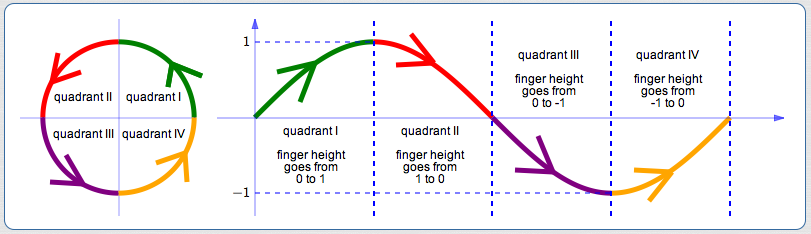
A Higher Level of Understanding for the Sine Function

In Radian Measure, we ‘wrap’ the real number line around the unit circle. In this way, every real number is associated with a point (called the terminal point) and a corresponding angle on the unit circle. The real number is then the radian measure of this angle!

Wrap the real number line around the unit circle!

Thus, every real number $\,x\,$ ...

... is associated with a point on the unit circle ...

... and a corresponding angle.

In The Unit Circle Approach to Trigonometry, we saw that $\,\sin(x)\,$ is the $y$-value of the terminal point:

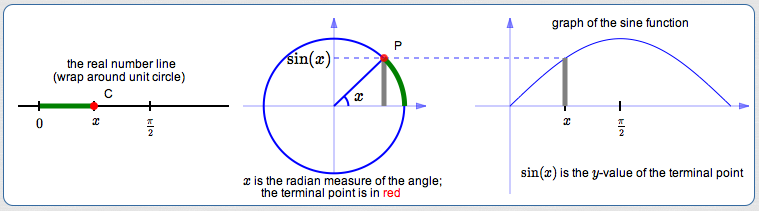
As $\,x\,$ goes from $\,0\,$ to $\,\frac{\pi}{2}\,,$ $\,\sin x\,$ goes from $\,0\,$ to $\,1\,.$
(Remember: $\,\frac{\pi}{2}\,$ radians is $\,90^\circ\,$)

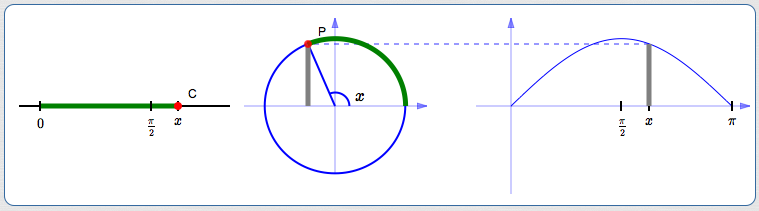
As $\,x\,$ goes from $\,\frac{\pi}{2}\,$ to $\,\pi\,,$ $\,\sin x\,$ goes from $\,1\,$ back to $\,0\,.$
(Remember: $\,\pi\,$ radians is $\,180^\circ\,$)

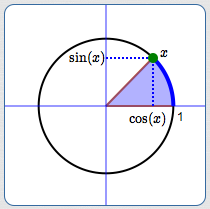
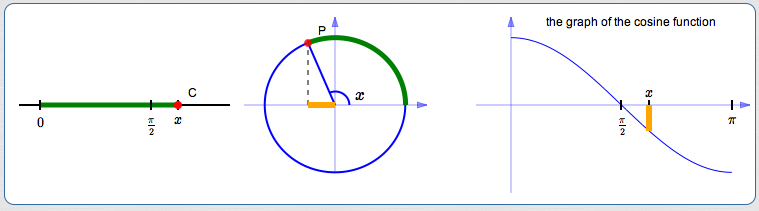
The Cosine Function

The entire discussion can be repeated to understand the cosine—except that it gives the $x$-values of the points, not the $y$-values!

Here's how one of the graphics above would be adjusted to focus attention on the $x$-value:

Important Characteristics of the Graphs

Properties of both sine and cosine:

Domain and Range

• Domain is $\Bbb R$  (Recall that $\,\Bbb R\,$ represents the set of real numbers.)
• Range is the interval $[-1,1]$

Period

• The period is $\,2\pi\,$

• Sine has period $\,2\pi\,$:  $\,\sin(x+2\pi) = \sin x\,$  for all real numbers $\,x\,.$

  More generally:  $\,\sin(x+2\pi k) = \sin x\,$  for all integers $\,k\,$ and all real numbers $\,x\,.$

• Cosine has period $\,2\pi\,$:  $\,\cos(x+2\pi) = \cos x\,$  for all real numbers $\,x\,.$

  More generally:  $\,\cos(x+2\pi k) = \cos x\,$  for all integers $\,k\,$ and all real numbers $\,x\,.$

Two Trigonometric Identities

Take the sine curve and shift it $\,\frac{\pi}{2}\,$ units to the left—it turns into the cosine curve:

Take the cosine curve and shift it $\,\frac{\pi}{2}\,$ units to the right—it turns into the sine curve:

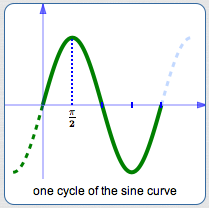
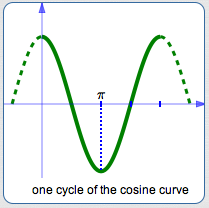
Thus, we have two new trigonometric identities! For all real numbers $\,x\,$: