GRAPHING GENERALIZED SINES AND COSINES,
LIKE $\,y = a\sin k(x\pm b)\,$ and $\,y = a\cos (kx\pm B)\,$

• PRACTICE (online exercises and printable worksheets)

The prior section explored the (basic) graphs of $\,y = \sin x\,$ and $\,y = \cos x\,$.
However, these trigonometric functions frequently appear in ‘transformed’ versions.
You might see, for example, $\,y = -1.5\sin \frac{1}{2}(x - \pi)\,$ or $\,y = \frac{1}{3}\cos (4x + 5)\,$.

The observations and techniques discussed in this section will allow you to reliably, quickly, and efficiently graph any function of the following forms, without memorizing a bunch of different formulas:

Notice, in particular, that the arguments $\,k(x\pm b)\,$ (first row) and $\,kx\pm B\,$ (second row) are different.
For example, $\,2(x-5)\,$ is different from $\,2x - 5\,$.
These input types are commonly seen in applications.

In mathematics, the word ‘argument’ is often used to refer to the input of a function.
For example, the argument of the sine function in the expression ‘$\,\sin k(x\pm b)\,$’ is $\,k(x\pm b)\,$.
As a second example, the argument of the cosine function in the expression ‘$\,\cos (kx\pm B)\,$’ is $\,kx\pm B\,$.

Any argument with only two types of terms—an $\,x\,$-term and a constant term—
can be handled with the four-step graphing process discussed below.
With this four-step technique, you don't need to identify which type of argument you're working with;
you only need to identify the coefficient of the $\,x\,$-term.

For example, the four-step technique can be used to graph (say) $\displaystyle\,y = -9\sin\frac{\pi + 5x}{8}\,$.
Why? The argument has only an $x$ term and a constant term.

Here, $\,k = \frac 58\,$.
Why? Rewrite the argument (as needed) to see that the coefficient of $\,x\,$ is $\,\color{red}{\frac 58}\,$: $$\frac{\pi +\color{red}{5}x}{\color{red}{8}} = \frac{\pi}8 + \color{red}{\frac{5}{8}}x\,$$

The following two key observations will lead to an efficient approach.
Click the show/hide buttons for additional information.

1. Observation #1:
   Each generalized function is the result of graphical transformation(s) chosen from:
   • horizontal stretch/shrink
   • shift right/left
   • vertical stretch/shrink
   • reflection about $x$-axis
   Here is a graphical example to illustrate.
   For clarity, only one period of each graph is shown.
   
   Keep in mind that transformations involving $\,x\,$ are counter-intuitive!
   For example, you might expect that replacing every $\,x\,$ by $\,\frac{x}{2}\,$ would result in the period being cut in half.
   In reality, the period is doubled! (Review earlier graphical transformation discussions to see why!)
   
   

   desired graph: $\,y = -1.5\sin \frac{1}{2}(x - \pi)\,$
   $y = \sin x$ (the basic model)	$y = \sin \frac{1}{2}x = \sin\frac{x}{2}$ Replace every $\,x\,$ by $\,\frac{x}{2}\,$. This gives a horizontal stretch: points $\,(x,y)\,$ move to $\,(2x,y)\,$.	$y = \sin\frac{1}{2}(x - \pi)$ Replace every $\,x\,$ by $\,x - \pi\,$. This shifts the graph $\,\pi\,$ to the right: points $\,(x,y)\,$ move to $\,(x+\pi,y)\,$.
   $y = 1.5\sin\frac{1}{2}(x - \pi)$ Multiply previous $\,y\,$-values by $\,1.5\,$. This gives a vertical stretch: points $\,(x,y)\,$ move to $\,(x,1.5y)\,$.	$y = -1.5\sin\frac{1}{2}(x - \pi)$ Multiply previous $y$-values by $\,-1\,$. This reflects about the $x$-axis: points $\,(x,y)\,$ move to $\,(x,-y)\,$.	The only transformation that changes the period is the horizontal stretch. In general, a horizontal stretch/shrink (replacing every $\,x\,$ by $\,kx\,$) causes points $\,(x,y)\,$ to move to $\displaystyle\,(\frac{x}{k},y)\,$. This changes a period of $\,2\pi\,$ to a new period of $\displaystyle\,\frac{2\pi}{k}\,$. In this example, $\,k = \frac{1}{2}\,$. Thus, the new period is: $\displaystyle\,\frac{2\pi}{k} = \frac{2\pi}{1/2} = 4\pi\,$

   
   
   Here is a second example, in tabular form:
   
   

   equation	do this to previous equation...	graphical result	one cycle of graph
   $y = \cos x$	(starting point)	basic model
   $y = \cos (x+5)$	replace every $\,x\,$ by $\,x+5\,$	shift left $\,5\,$, $\,(x,y)\mapsto (x-5,y)$
   $y = \cos (4x+5)$	replace every $\,x\,$ by $\,4x\,$	horizontal shrink, $\,(x,y)\mapsto (\frac x4,y)$ (This is the only step that changes the period.)
   $y = \frac 13\cos (4x+5)$	multiply previous $y$-value by $\,\frac 13\,$	vertical shrink, $\,(x,y)\mapsto (x,\frac 13y)$

2. Observation #2:
   The only transformation that changes the period is the the horizontal stretch/shrink.
   
   The horizontal stretch/shrink is caused by replacing every $\,x\,$ by $\,kx\,$,
   which causes points $\,(x,y)\,$ to move to new points $\displaystyle\,(\frac{x}{k},y)\,$.
   
   For $\,k > 0\,$, the horizontal stretch/shrink changes the original period $\,2\pi\,$ to the new period $\displaystyle\,\frac{2\pi}{k}\,$.
   
   If $\,k < 0\,$, rewrite first, using (as needed):
   • sine is odd:   $\,\sin(-x) = -\sin x\,$
     
     Graph:   $y = \sin (3 - x)\,$
     (Note that the coefficient of $\,x\,$ is $\,-1\,$.)
     
     So, rewrite:
     

     $\sin(3-x)$	$=$	$\sin \bigl(-(x-3)\bigr)$	(factor out $\,-1\,$)
     	$=$	$-\sin (x-3)\,$	(sine is odd)

     
     Now, graph the equivalent equation: $\,y = -\sin (x-3)\,$
   • cosine is even:   $\,\cos (-x) = \cos x$
     
     Graph:   $y = \cos (-5x+3))\,$
     (Note that the coefficient of $\,x\,$ is $\,-5\,$.)
     
     So, rewrite:
     

     $\cos(-5x+3)$	$=$	$\cos \bigl(-(5x-3)\bigr)$	(factor out $\,-1\,$)
     	$=$	$\cos (5x-3)\,$	(cosine is even)

     
     Now, graph the equivalent equation: $\,y = \cos (5x-3)\,$

THE FOUR-STEP GRAPHING PROCESS:

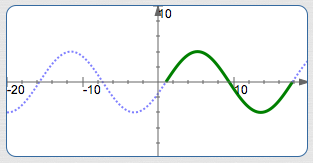
GENERAL PROCEDURE	EXAMPLE:   Graph $\,y = -7\cos (3-5x)\,$
STEP 1:   CHECK THAT $\,k\,$ IS POSITIVE The coefficient of the $\,x\,$-term in the argument is denoted by $\,k\,$. Make sure that $\,k > 0\,$. If not, rewrite (as above), using the odd/even properties of sine/cosine.	Initially, the coefficient of the $\,x\,$ term is $\,-5\,$. Rewrite: $$\,-7\cos (3-5x)\ \ \underset{\text{law}}{\overset{\text{distributive}}{=}}\ \ -7\cos\bigl(-(5x-3)\bigr) \ \ \underset{\text{is even}}{\overset{\text{cosine}}{=}}\ \ -7\cos (5x-3)$$ Instead, graph:   $y = -7\cos (5x-3)$ (So, $\,k = 5\,$.)
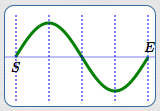
STEP 2:   STARTING POINT Each sine/cosine curve starts a ‘natural’ cycle when its argument is zero. Compute the value of $\,x\,$ that makes the argument equal to zero. This is your starting point; call it $\,S\,$ and mark it on a number line.	Find $\,S\,$: $$ \begin{gather} 5x-3 = 0\cr 5x = 3\cr x = \frac{3}{5} \end{gather} $$ So, $\,S = \frac{3}{5}\,$.
STEP 3:   ENDING POINT Compute the new period, $\displaystyle\,\frac{2\pi}{k}\,$. The cycle that starts at $\,S\,$ ends at $\displaystyle\,E := S +\frac{2\pi}{k}\,$. In other words, one complete cycle occurs on the interval $\,[S,\underbrace{S +\frac{2\pi}{k}}_{E}]\,$. Mark the ending point, $\,E\,$, on the number line. Divide the interval from STARTING POINT to ENDING POINT into four equal parts, to make it easier to draw in the basic cycle.	$\,k = 5\,$ $\displaystyle\text{period} = \frac{2\pi}{k} = \frac{2\pi}{5}$ $\displaystyle E := S + \frac{2\pi}{k} = \frac{3}{5} + \frac{2\pi}{5}$
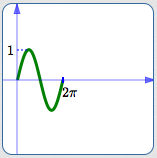
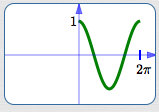
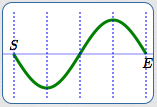
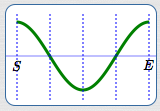
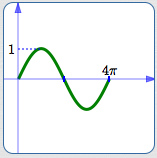
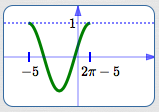
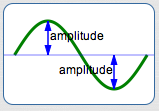
STEP 4:   DRAW IN THE BASIC CYCLE; ADJUST (AS NEEDED) FOR AMPLITUDE/FLIP basic sine cycle basic cosine cycle As discussed in the next section, amplitude is the distance from the $x$-axis to the highest (or lowest) part of the graph. The amplitude of $\,y = \sin x\,$ and $\,y = \cos x\,$ is $\,1\,$. Vertical scaling by a factor of $\,a\,$ causes the amplitude to change to $\,|a|\,$. Vertical scaling by a factor of $\,-1\,$ causes reflection about the $x$-axis (i.e., a ‘flip’). 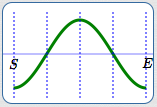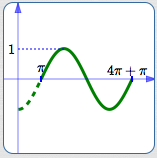basic sine cycle, flipped basic cosine cycle, flipped	Draw in the basic cosine cycle, flipped. The amplitude is $\,7\,$. 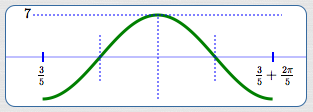To emphasize: In this graph of (one cycle of) $y = -7\cos (5x-3)$: the fact that it is a cosine curve, $\,y = -7\color{red}{\cos}(5x-3)\,$, causes you to use the basic cosine cycle; the leading minus sign, $\,{\bf\color{red}{-}}7\,$, causes the cycle to be flipped; the amplitude is $\,|-7|\, = 7\,$

EXAMPLES

The three earlier examples are repeated, using a compact version of the four-step graphing process.
A new example is also given.
See how quick and easy it is!

In these examples, cycles are shown in a standard viewing window ($\,x\,$ between $\,-20\,$ and $\,20\,$; $\,y\,$ between $\,-10\,$ and $\,10\,$),
to make comparisons between graphs easier.
The cycle being graphed with the four-step process is shown in dark green.
Additional cycles are shown to complete the viewing window.
Decimal approximations to the tenths place are included.
Remember to get exact answers first, then approximate!

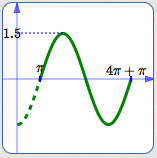
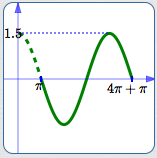
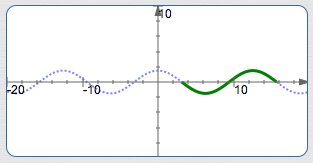
Graph $\,y = -1.5\sin\frac12(x-\pi)\,$ using the four-step process

1. $k = \frac 12 = 0.5$
2. $S = \pi \approx 3.1$
   (mentally set $\,\frac 12(x-\pi)\,$ equal to zero)
3. $\displaystyle\text{period} = \frac{2\pi}{k} = \frac{2\pi}{0.5} = 4\pi \approx 12.6 $
   $E = S + \text{period} = \pi + 4\pi = 5\pi \approx 15.7$
4. basic sine cycle, flipped, on about $\,[3.1,15.7]\,$, amplitude is $\,1.5\,$:
   
   

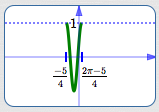
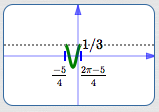
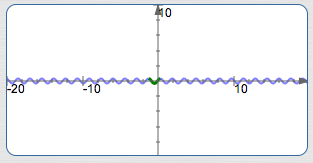
Graph $\,y = \frac13\cos (4x+5)\,$ using the four-step process

1. $k = 4$
2. $S = -\frac{5}{4} = -1.25$
   (mentally set $\,4x+5\,$ equal to zero)
3. $\displaystyle\text{period} = \frac{2\pi}{k} = \frac{2\pi}{4} = \frac{\pi}{2} \approx 1.6$
   $\displaystyle\displaystyle E = S + \text{period} = -1.25 + \frac{\pi}2 \approx 0.3$
4. basic cosine cycle on (about) $\,[-1.25,0.3]\,$, amplitude is $\displaystyle\,\frac{1}{3}\,$:
   
   

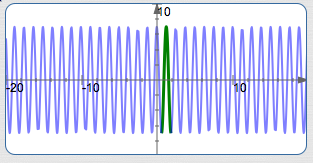
Graph $\,y = -7\cos (3 - 5x)\,$ using the four-step process

1. Rewrite: $-7\cos(3-5x) = -7\cos(-(5x-3)) = -7\cos(5x-3)$
   (cosine is even)
   $k = 5$
2. $S = \frac{3}{5} = 0.6$
   (mentally set $\,5x-3\,$ equal to zero)
3. $\displaystyle\text{period} = \frac{2\pi}{5} = 0.4\pi \approx 1.3 $
   $E = S + \text{period} = 0.6 + 0.4\pi \approx 1.9$
4. basic cosine cycle, flipped, on about $\,[0.6,1.9]\,$, amplitude is $\,7\,$:
   

Graph $\displaystyle\,y = -4\sin\frac{\pi-3x}{8} \,$ using the four-step process

1. Rewrite: $\displaystyle -4\sin\frac{\pi-3x}{8} = -4\sin (-\frac 18(3x-\pi)) = 4\sin\frac18(3x - \pi)$
   (sine is odd)
   $\displaystyle k = \frac38 \approx 0.4$
2. $\displaystyle S = \frac{\pi}{3} \approx 1.0$
   (mentally set $\displaystyle\,\frac18(3x-\pi)\,$ equal to zero)
3. $\displaystyle\text{period} = \frac{2\pi}{3/8} = \frac{16\pi}3 \approx 16.8 $
   $\displaystyle E = S + \text{period} = \frac{\pi}3 + \frac{16\pi}3 = \frac{17\pi}3 \approx 17.8$
4. basic sine cycle on about $\,[1.0,17.8]\,$, amplitude is $\,4\,$: