 Using a Function Box Backwards
Using a Function Box Backwards
Recall that a function can be viewed as a ‘box’: you drop an input in the top, the function does something to the input, and a unique output drops out the bottom.
In this lesson, we're going to try and use a function box ‘backwards’. That is, we'll pick up a number from the output pile, put it in the box ‘backwards’, and try to see what input it came from.
Sometimes this works out nicely, and sometimes it doesn't!
The Squaring Function: Using the Function Box ‘Backwards’ Fails
Consider the squaring function, $\,f(x) = x^2\,.$
Note:
- $\,f(2) = 2^2 = 4\,$
- $\,f(-2) = (-2)^2 = 4\,$
In other words:
- Drop a $\,2\,$ in the top, and $\,4\,$ comes out the bottom.
- Drop a $\,-2\,$ in the top, and again $\,4\,$ comes out the bottom.
Now, pick up the number $\,4\,$ from the output pile. What input did it come from? Did it come from the input $\,2\,$? Did it come from the input $\,-2\,$? There's no way to know!
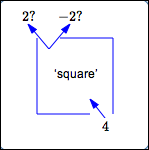
The output $\,4\,$ does not have a unique corresponding input. Indeed, in this case, the output $\,4\,$ has two corresponding inputs, as the graph of the squaring function clearly shows.
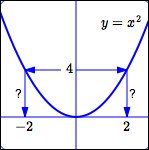
For the squaring function, trying to use the function box ‘backwards’ fails.
The Cubing Function: Using the Function Box ‘Backwards’ Succeeds
Consider the cubing function, $\,f(x) = x^3\,.$
Note:
- $\,f(2) = 2^3 = 8\,$
- There is no other input whose output is $\,8\,.$
Pick up the number $\,8\,$ from the output pile. What input did it come from? It came from the input $\,2\,.$ The output $\,8\,$ has a unique corresponding input.
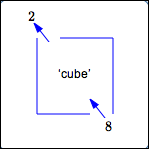
Since every real number has a unique cube root, every output from the cubing function has a unique corresponding input.
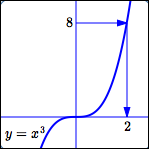
For the cubing function, using the function box ‘backwards’ succeeds.
So—When Can a Function Box Be Used ‘Backwards’?
A function box can only be used ‘backwards’ when every output has exactly one corresponding input!
The Horizontal Line Test: A Graphical Test to See if Each Output Has Exactly One Corresponding Input
Imagine sweeping a horizontal line from top to bottom (or bottom to top) through the graph of a function.
At each location, the horizontal line hits the $y$-axis (but not necessarily the graph of the function!) in a unique point. You're ‘testing’ each output to see how many corresponding input(s) it has.
If a horizontal line ever hits the graph at more than one point (as in the squaring function), then there exists an output with more than one input.
For the squaring function, the horizontal line at height $\,4\,$ hits the graph at two points: $\ x=2\ $ and $\ x=-2\ .$ In this case, we say that the graph ‘fails the horizontal line test’.
If a horizontal line always intersects the graph at only one point, then every output has only one input. In this case, we say that the graph ‘passes the horizontal line test’. For example, the graph of the cubing function passes the horizontal line test.
Summary: One-To-One Functions
So—some functions are ‘nicer’ than others, with respect to using the function box ‘backwards’!
Which are the ‘nice’ ones? The ones with graphs that pass a horizontal line test!
(Note: Every function already passes a vertical line test.)
For these ‘nice’ functions, there is a beautiful relationship between the inputs and outputs. Since it's a function, each input has exactly one output (that is, the graph passes a vertical line test). Since it additionally passes a horizontal line test, each output has exactly one input.
Put together, it is as if the inputs and outputs are connected with strings! Pick up any input, follow the string to its unique corresponding output. Pick up any output, follow the string back to its unique corresponding input.
There is a one-to-one correspondence between the inputs and outputs. An input uniquely determines an output, and an output uniquely determines an input.
In the next lesson, we'll give these ‘nice’ functions a special name: one-to-one functions. Soon after, we'll see that one-to-one functions have inverses that ‘undo’ what the function does, and we'll study techiques for finding inverses.