 Double Angle Formulas for Sine and Cosine
Double Angle Formulas for Sine and Cosine
The double-angle formulas for sine and cosine tell how to find the sine and cosine of twice an angle ($\,2x\,$), in terms of the sine and cosine of the original angle ($\,x\,$).
Double-Angle Formula for the Sine
$$\cssId{s4}{\sin 2x = 2\sin x\,\cos x}$$Double-Angle Formulas for the Cosine
Three versions:
$$ \cssId{s7}{ \begin{align} \cos 2x &=\cos^2 x - \sin^2 x\cr\cr \cos 2x &= 1 - 2\sin^2 x\cr\cr \cos 2x &= 2\cos^2 x - 1 \end{align}} $$Notes on the Double-Angle Formulas
They're Identities
The double-angle formulas are identities. That is, they are always true. They could each be prefaced with: ‘For all real numbers $\,x\,$ ... ’
Function Notation Convention
Recall the convention regarding the use of function notation with multi-letter function names (like ‘$\,\sin\,$’ and ‘$\,\cos\,$’): parentheses can be dropped, as long as there is no confusion about order of operations.
Thus, you typically see ‘$\,\sin 2x\,$’ (no parentheses) instead of ‘$\,\sin(2x)\,$’ (with parentheses).
Both ‘$\,\sin 2x\,$’ and ‘$\,\sin(2x)\,$’ represent the same thing:
- The function name is ‘$\,\sin\,$’ (pronounced ‘sine’, long i).
- The input to the function is $\,2x\,.$
- Both ‘$\,\sin 2x\,$’ and ‘$\,\sin(2x)\,$’ represent the output from the function ‘$\,\sin\,$’ when the input is $\,2x\,.$
Notation for Squaring Sine and Cosine
Recall that ‘$\,\sin^2 x\,$’ is a shorthand for $\,(\sin x)^2\,,$ which equals $\,(\sin x)(\sin x)\,.$
Similarly, ‘$\,\cos^2 x\,$’ is a shorthand for: $$(\cos x)^2 = (\cos x)(\cos x)$$
Verbalizing the Double-Angle Formulas
Here is a verbalization of the double-angle formula for the sine:
$$ \begin{align} &\cssId{s22}{\overbrace{\sin\strut}^{\text{ the sine }}}\ \ \cssId{s23}{\overbrace{(2x)\strut}^{\text{ of twice an angle }}}\cr\cr &\qquad\cssId{s24}{\overbrace{=\strut}^{\text{ is }}}\ \ \cssId{s25}{\overbrace{\strut 2}^{\text{ twice }}} \cssId{s26}{\overbrace{\strut \sin x}^{\text{ the sine of the original angle }}}\cr\cr &\qquad\qquad\ \ \cssId{s27}{\overbrace{\cdot\strut}^{\text{ times }}} \cssId{s28}{\overbrace{\strut \cos x}^{\text{ the cosine of the original angle }}} \end{align} $$Here is a verbalization of a double-angle formula for the cosine. The other two versions can be similarly verbalized.
$$ \begin{align} &\cssId{s31}{\overbrace{\cos\strut}^{\text{ the cosine }}}\ \ \cssId{s32}{\overbrace{(2x)\strut}^{\text{ of twice an angle }}}\cr\cr &\qquad\cssId{s33}{\overbrace{=\strut}^{\text{ is }}}\ \ \cssId{s34}{\overbrace{\strut 1}^{\text{ one }}} \cssId{s35}{\overbrace{-\strut}^{\text{ minus }}}\cr\cr &\qquad\qquad\ \ \cssId{s36}{\overbrace{2\strut}^{\text{ twice }}} \cssId{s37}{\overbrace{\sin^2\strut}^{\text{ the sine squared }}} \cssId{s38}{\overbrace{(x)\strut}^{\text{ of the original angle}}} \end{align} $$How to Refer to the Cosine Double-Angle Formulas
In this section, the three versions of the double-angle formula for the cosine are referred to as follows:
| $\cos 2x = \cos^2 x - \sin^2 x$ | the version involving both sine and cosine |
| $\cos 2x = 1 - 2\sin^2 x$ | the version involving only the sine |
| $\cos 2x = 2\cos^2 x - 1$ | the version involving only the cosine |
Note that these descriptions refer to what is happening on the right-hand side of the formulas.
Derivations of the Double-Angle Formulas
The double-angle formulas are simple to prove, once the Addition Formulas for Sine and Cosine are in place.
For all real numbers $\,x\,$:
$$ \begin{align} \cssId{s50}{\sin 2x\ } &\cssId{s51}{=} \cssId{s52}{\ \sin (x + x)}\cr &\qquad\cssId{s53}{\text{(rename $\,2x\,$ as $\,x + x\,$)}}\cr\cr &\cssId{s54}{=} \cssId{s55}{\ \sin x\,\cos x + \cos x\,\sin x}\cr &\qquad\cssId{s56}{\text{(the Sine Addition Formula)}}\cr\cr &\cssId{s57}{=} \cssId{s58}{\ 2\sin x\,\cos x}\cr &\qquad\cssId{s59}{\text{(add like terms)}} \end{align} $$$$ \begin{align} \cssId{s60}{\cos 2x\ } &\cssId{s61}{=} \cssId{s62}{\ \cos (x + x)}\cr &\qquad\cssId{s63}{\text{(rename $\,2x\,$ as $\,x + x$)}}\cr\cr &\cssId{s64}{=} \cssId{s65}{\ \cos x\,\cos x - \sin x\,\sin x}\cr &\qquad\cssId{s66}{\text{(the Cosine Addition Formula)}}\cr\cr &\cssId{s67}{=} \cssId{s68}{\ (\cos x)^2 - (\sin x)^2}\cr &\qquad\cssId{s69}{\text{(exponent notation)}}\cr\cr &\cssId{s70}{=} \cssId{s71}{\ \cos^2 x - \sin^2 x}\cr &\qquad\cssId{s72}{\text{(shorthand notation)}} \end{align} $$
By the Pythagorean Identity, $\,\cos^2 x = 1 - \sin^2 x\,$ and $\,\sin^2 x = 1 - \cos^2 x\,.$ Thus, we get two alternative versions of the cosine double angle formula:
$$ \begin{align} \cssId{s75}{\cos 2x\ \ } &\cssId{s76}{= \ \cos^2 x - \sin^2 x}\cr\cr &\cssId{s77}{= \ (1 - \sin^2 x) - \sin^2 x} \cr\cr &\cssId{s78}{= \ 1 - 2\sin^2 x} \end{align} $$and
$$ \begin{align} \cssId{s80}{\cos 2x\ \ } &\cssId{s81}{= \ \cos^2 x - \sin^2 x} \cr\cr &\cssId{s82}{= \ \cos^2 x - (1 - \cos^2 x)} \cr\cr &\cssId{s83}{= \ \cos^2 x - 1 + \cos^2 x} \cr\cr &\cssId{s84}{= \ 2\cos^2 x - 1} \end{align} $$A Geometric Proof of the Double-Angle Formulas, For Small Angles
For the sketch and derivation below, assume $\,x\,$ is measured in degrees and $\,2x \lt 90^\circ\,.$
This is a different ‘stacking’ of triangles than in the prior lesson, to show alternative proof approaches.
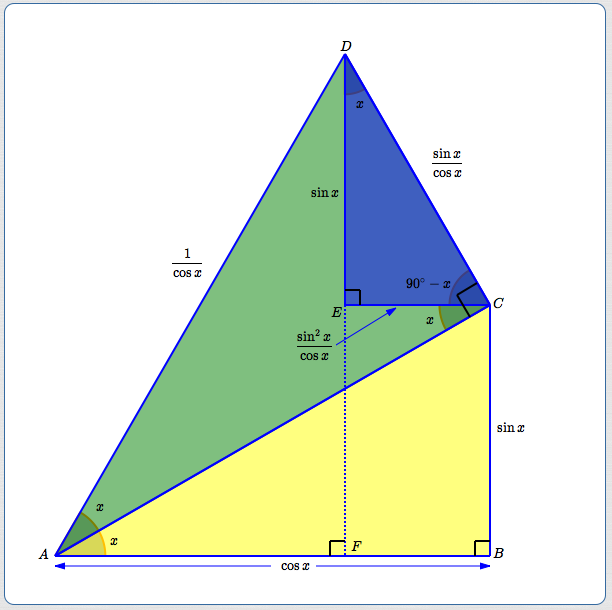
Start with right triangle $\,\triangle ABC\,$ (yellow). It has acute angle $\,x\,$ and hypotenuse of length $\,1\,.$
- Bottom leg: $\,\cos x\,$
- Side leg: $\,\sin x\,$

Stack a right triangle $\,\triangle ACD\,$ (mostly green) on the hypotenuse of the yellow triangle. It also has acute angle $\,x\,.$ The bottom leg has length $\,1\,.$
- Since $\,\cos x = \frac{\text{ADJ}}{\text{HYP}} = \frac{1}{\text{HYP}}\,,$ the hypotenuse has length $\,\frac{1}{\cos x}\,.$ (Solve for $\,\text{HYP}\,.$)
- Thus, the side leg is $\,\frac{1}{\cos x}\cdot \sin x = \frac{\sin x}{\cos x}\,.$

The blue right triangle:
- Since $\,\overline{EC}\, ||\, \overline{AB}\,,$ $\,\angle ACE = x\,$ (alternate interior angles).
- Thus, $\,\angle ECD = 90^\circ - x\,.$
- Thus, $\,\angle EDC = x\,.$
- Bottom leg: $\,\displaystyle\frac{\sin x}{\cos x}(\sin x) = \frac{\sin^2 x}{\cos x}\,$
- Side leg: $\,\displaystyle\frac{\sin x}{\cos x}(\cos x) = \sin x\,$

Using right triangle $\,\triangle AFD\,,$ we get the cosine double-angle formula:
$$ \begin{align} \cssId{s112}{\cos 2x\ \ } &\cssId{s113}{= \frac{\text{ADJ}}{\text{HYP}}}\cr\cr &\cssId{s114}{= \frac{\cos x - \frac{\sin^2 x}{\cos x}}{1/\cos x}}\cr\cr &\cssId{s115}{= \left(\cos x - \frac{\sin^2 x}{\cos x}\right)(\cos x)}\cr\cr &\cssId{s116}{= \ \cos^2 x - \sin^2 x}\cr\cr \end{align} $$
Again using right $\,\triangle AFD\,,$ we get the sine double-angle formula:
$$ \begin{align} \cssId{s119}{\sin 2x\ \ } &\cssId{s120}{=\ \frac{\text{OPP}}{\text{HYP}}} \cr\cr &\cssId{s121}{=\ \frac{\sin x +\sin x}{1/\cos x}} \cr\cr &\cssId{s122}{=\ 2\sin x\,\cos x} \end{align} $$Review: Does $\,\cos x\,$ Uniquely Determine $\,\sin x\,$? No!
Recall that every nonzero real number is uniquely identified by knowing two things:
- its size (distance from zero)
- its sign (plus or minus)
This fact is often crucial when working with trigonometric expressions.
Often, knowing the value of a trigonometric expression (like $\,\cos x\,$) allows you to correctly determine the size of other trigonometric expressions, but not the sign. Additional information must be provided to get the correct sign.
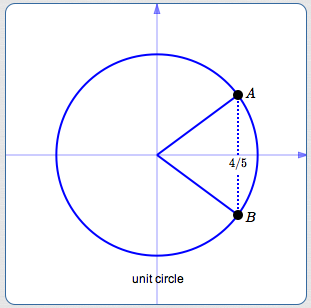
For example, suppose you know that $\,\cos x = \frac 45\,,$ and nothing else. Does this allow us to uniquely determine $\,\sin x\,$? No! It gives the size of $\,\sin x\,,$ but not the sign, as follows:
- Knowing $\,\cos x = \frac 45\,$ puts the terminal point for $\,x\,$ in either quadrant I (point $\,A\,$) or quadrant IV (point $\,B\,$), as shown above.
-
Finding the size of $\,\sin x\,$ is routine. For example, you can use the Pythagorean Identity:
$$ \begin{align} \cssId{s141}{\sin^2 x\ \ } &\cssId{s142}{=\ 1 - \cos^2 x} \cr\cr &\cssId{s143}{=\ 1 - \left(\frac 45\right)^2} \cr\cr &\cssId{s144}{=\ \frac{25}{25} - \frac{16}{25}}\cr\cr &\cssId{s145}{=\ \frac{9}{25}} \end{align} $$Thus, $\sin x = \pm \frac{3}{5}\,.$ The size of $\,\sin x\,$ is $\,\frac 35\,.$ The sign is unknown (without additional information).
There is a variety of additional information that might be given to determine the sign of $\,\sin x\,.$ Here are some examples:
Sign of $\,\sin x\,$ is Positive
$\,x\,$ is in Quadrant I
$\,\sin x\,$ is positive
$\csc x \gt 0$
Cosecant is the reciprocal of the sine. If cosecant is positive, so is sine: $\,\sin x\,$ is positive.
$\tan x \gt 0$
Tangent is sine over cosine. If cosine is positive and tangent is positive, then $\,\sin x\,$ is positive.
Sign of $\,\sin x\,$ is Negative
$\,x\,$ is in Quadrant IV
$\,\sin x\,$ is negative
$\csc x \lt 0$
Cosecant is the reciprocal of the sine. If cosecant is negative, so is sine: $\,\sin x\,$ is negative.
$\tan x \lt 0$
Tangent is sine over cosine. If cosine is positive and tangent is negative, then $\,\sin x\,$ is negative.
Example: Using the Double-Angle Formulas
Suppose that $\displaystyle\,\cos x = \frac 45\,$ and $\,\csc x \lt 0\,.$ Find $\,\sin 2x\,,$ $\,\cos 2x\,,$ and $\,\tan 2x\,.$
Solution
By the Pythagorean Identity:
$$ \begin{align} \cssId{s180}{\sin^2 x\ \ } &\cssId{s181}{=\ 1 - \cos^2 x} \cr\cr &\cssId{s182}{=\ 1 - \left(\frac 45\right)^2} \cr\cr &\cssId{s183}{=\ \frac{25}{25} - \frac{16}{25}}\cr\cr &\cssId{s184}{=\ \frac{9}{25}} \end{align} $$So, $\, \sin x = \pm \frac{3}{5}\,.$ Since $\,\csc x := \frac{1}{\sin x} \overbrace{\lt}^{\text{given}} 0\,,$ we have $\,\sin x \lt 0\,.$ Together, $\,\sin x = -\frac{3}{5}\,.$
$$ \begin{align} \cssId{s189}{\sin 2x\ \ } &\cssId{s190}{=\ 2\sin x\,\cos x} \cr\cr &\cssId{s191}{=\ 2\bigl(-\frac 35\bigr)\bigl(\frac 45\bigr)} \cr\cr &\cssId{s192}{=\ \color{blue}{-\frac{24}{25}}} \end{align} $$$$ \begin{align} \cssId{s193}{\cos 2x\ \ } &\cssId{s194}{=\ 2\cos^2 x - 1}\cr\cr &\cssId{s195}{=\ 2\left(\frac 45\right)^2 - 1} \cr\cr &\cssId{s196}{=\ 2\cdot\frac{16}{25} - \frac{25}{25}}\cr\cr &\cssId{s197}{=\ \color{red}{\frac{7}{25}}} \end{align} $$
(Any of the three cosine double-angle formulas can be used. The one chosen here is ‘safest’ since it uses only given—not computed—information.)
$$ \begin{align} \cssId{s200}{\tan 2x\ \ } &\cssId{s201}{:=\ \frac{\sin 2x}{\cos 2x}}\cr\cr &\cssId{s202}{=\ \frac{\color{blue}{-\frac{24}{25}}}{\color{red}{\frac{7}{25}}}\cdot \frac{25}{25}}\cr\cr &\cssId{s203}{=\ -\frac{24}{7}} \end{align} $$Complex Fractions
A complex fraction is an expression that involves ‘fractions within fractions’, like: $\,\displaystyle\frac{-\frac{24}{25}}{\frac{7}{25}}$
Here is a technique used to transform a complex fraction to a simple fraction:
- Find the least common denominator (LCD) of all the simple fractions involved.
- Multiply the complex fraction by $\,1\,$ in the form of $\,\frac{\text{LCD}}{\text{LCD}}\,.$
This is a beautiful example of ‘multiplying by $\,1\,$ in an appropriate form’! Here's how this technique was applied above:
- The top fraction ($\,-\frac{24}{25}\,$) has denominator $\,25\,.$
- The bottom fraction ($\,\frac{7}{25}\,$) also has denominator $\,25\,.$
- The least common multiple of $\,25\,$ and $\,25\,$ is $\,25\,.$ Thus, the LCD of all the simple fractions involved is $\,25\,.$
- The complex fraction was multipled by $\,\frac{\text{LCD}}{\text{LCD}} = \frac{25}{25}\,,$ and all the ‘little’ fractions disappeared!