 Combining Functions to get New Functions
Combining Functions to get New Functions
Numbers can be ‘connected’ to get new numbers: for example, $\,1+2=3\,.$ Indeed, addition ‘+’ is a connective for numbers.
Sets can be ‘connected’ to get new sets: for example, $\,\{1,2,3\}\cap \{2\} = \{2\}\,.$ Indeed, the intersection operator ‘$\,\cap\,$’ is a connective for sets.
Functions can also be ‘connected’ to get new functions: the most important way to do this, called function composition, is the subject of the next lesson. In this lesson, we look at some other ways that functions can be combined to get new functions.
The Sum Function
Consider the box below:
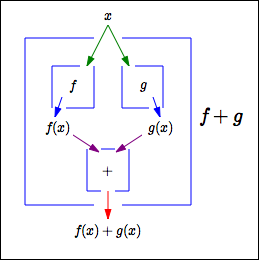
It shows how two functions $\,f\,$ and $\,g\,$ are ‘combined’ to get a new function, named $\,f+g\,.$
(Don't be intimidated by the multi-symbol function name ‘$\,f+g\,$’! It's a very natural name, as you'll see.)
Here's how this new function $\,f+g\,$ works:
- Drop an input $\,x\,$ in the top.
- This input gets ‘copied’: one copy gets dropped in the $\,\color{green}{f}\,$ box, the other in the $\,\color{green}{g}\,$ box.
- The two outputs $\,\color{purple}{f(x)}\,$ and $\,\color{purple}{g(x)}\,$ get dropped in the ‘+’ box, which adds them.
- The number $\,\color{red}{f(x) + g(x)}\,$ comes out the bottom.
Thus, $\,(f+g)(x) := f(x) + g(x)\,.$
$$ \cssId{s22}{(} \overbrace{\strut \cssId{s23}{f+g}}^{\cssId{s25}{\text{this function}}}\cssId{s24}{)} \cssId{s26}{(}\overbrace{\strut \ \ \cssId{s27}{x}\ \ }^{\cssId{s29}{\text{acts on } x}}\cssId{s28}{)} \overbrace{\strut \ \ \cssId{s30}{:=}\ \ }^{\cssId{s31}{\text{and gives}}} \overbrace{\strut \cssId{s32}{f(x) + g(x)}}^{\cssId{s33}{\text{this output}}} $$When using function notation, parentheses should always be put around the function name $\,f+g\,$ for clarity. Remember that ‘$\,:=\,$’ means ‘equals, by definition’.
The domain of $\,f+g\,$ is the set of all inputs that both $\,f\,$ and $\,g\,$ know how to act on. This is all we have to worry about—after getting the outputs $\,f(x)\,$ and $\,g(x)\,,$ any two real numbers can be added.
$$ \begin{align} &\cssId{s40}{\text{dom}(f+g)}\cr\cr &\quad\cssId{s41}{= \{x\ |\ x\in\text{dom}(f) \text{ and } x\in\text{dom}(g)\}}\cr\cr &\quad\cssId{s42}{= \{x\ |\ x\in \bigl(\text{dom}(f) \cap \text{dom}(g)\bigr)\}}\cr\cr &\quad\cssId{s43}{= \text{dom}(f) \cap \text{dom}(g)} \end{align} $$Difference, Product, and Quotient Functions
The idea is the same for the difference, product, and quotient functions:
| Function: | $f - g$ |
| Definition: | $(f-g)(x) := f(x) - g(x)$ |
| Domain: | $\text{dom}(f-g) = \text{dom}(f) \cap \text{dom}(g)$ |
| Function: | $fg$ |
| Definition: | $(fg)(x) := f(x)g(x)$ |
| Domain: | $\text{dom}(fg) = \text{dom}(f) \cap \text{dom}(g)$ |
| Function: | $\displaystyle\frac{f}{g}$ |
| Definition: | $\displaystyle\bigl(\frac{f}{g}\bigr)(x) := \frac{f(x)}{g(x)}$ |
| Domain: | |
|
$$
\text{dom}\bigl(\frac{f}{g}\bigr)
= \text{dom}(f) \cap \text{dom}(g)
\cap \{x\ |\ g(x)\ne 0\}
$$
|
|
| Since division by zero is not allowed, the domain of the quotient function is a bit more complicated. | |
Example
Let $\,f(x) = x^2\,$ and $\,g(x) = x+3\,.$
Find $\,f+g\,,$ $\,f-g\,,$ $\,fg\,,$ and $\,\frac{f}{g}\,.$
Solution:
$$ \begin{align} \cssId{s63}{(f+g)(x)}\ &\cssId{s64}{:= f(x) + g(x)}\cr &\cssId{s65}{ = x^2 + x + 3}\cr \cr \cssId{s66}{(f-g)(x)}\ &\cssId{s67}{:= f(x) - g(x)}\cr &\cssId{s68}{ = x^2 - (x + 3)}\cr &\cssId{s69}{ = x^2 - x - 3}\cr \cr \cssId{s70}{(fg)(x)}\ &\cssId{s71}{:= f(x)g(x)}\cr &\cssId{s72}{ = x^2(x+3)}\cr &\cssId{s73}{ = x^3 + 3x^2}\cr \cr \cssId{s74}{\bigl(\frac{f}{g}\bigr)(x)}\ &\cssId{s75}{:= \frac{f(x)}{g(x)}}\cr &\cssId{s76}{ = \frac{x^2}{x+3}}\cssId{s77}{\ \ \text{for}\ \ x\ne -3} \end{align} $$