audio read-through Circles and the Completing the Square Technique

Circles are useful in many Precalculus and Calculus problems (and in life). For a thorough review, study the following two lessons. Be sure to click-click-click the web exercises in each lesson to check your understanding!

For those of you who are short on time, however, a quick review is offered below. It might be all that you need!

EQUATIONS OF CIRCLES (standard form)
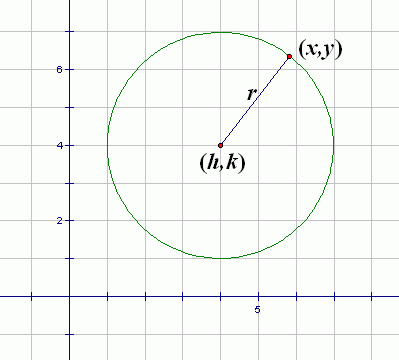
The equation of the circle with center $\,(h,k)\,$ and radius $\,r\,$ is: $$ \cssId{s12}{(x-h)^2 + (y-k)^2 = r^2} $$ This form of the equation is often called the standard form of a circle.
circle with center (h,k) and radius r

For example, the circle with center $\,(2,-3)\,$ and radius $\,5\,$ might make its appearance in any of these equivalent forms:

$$ \begin{gather} \cssId{s15}{(x - 2)^2 + (y - (-3))^2 = 5^2}\cr\cr \cssId{s16}{x^2 - 4x + y^2 + 6y = 12}\cr\cr \cssId{s17}{(x-2)^2 + (y+3)^2 = 25}\cr\cr \cssId{s18}{x^2 + 6y = 12 + 4x - y^2}\cr\cr \cssId{s19}{x^2 - 4x + 4 + y^2 + 6y + 9 = 25}\cr\cr \cssId{s20}{2x^2 + 12y = 24 + 8x - 2y^2} \end{gather} $$

You need to be able to recognize any of these equations as a circle, and then put it in standard form and graph it. Here are the tools you need:

RECOGNIZING CIRCLES (when they're not in standard form)

Let $\,b\,,$ $\,c\,,$ and $\,d\,$ be real numbers, and let $\,a\,$ be a nonzero real number.

Equations of the form

$$\cssId{s29}{ax^2 + ay^2+bx+cy=d}$$

graph as circles.

You must have both $\,x^2\,$ and $\,y^2\,$ terms, and they must have the same coefficient, when they are on the same side of the equation.

You are allowed (but not required) to have $\,x\,,$ $\,y\,,$ and constant terms.

You may not have any other term types.

It is possible to end up with a circle with radius zero, sometimes called a ‘point’ circle, like $\,x^2+y^2 = 0\,.$ The only solution to this equation is $\,(0,0)\,.$

It is also possible to end up with an ‘imaginary’ circle, like $\,x^2 + y^2 = -1\,.$ In this case, there are no real numbers $\,x\,$ and $\,y\,$ that make the equation true.

The technique of ‘completing the square’ is needed to put a circle in standard form:

COMPLETING THE SQUARE TECHNIQUE

The process of finding the correct number to add to an expression of the form $\ x^2+bx\ $ to form a perfect square trinomial is called completing the square.

The correct number to add is:

$$\cssId{s50}{ {\left(\frac{b}{2}\right)}^2}$$

That is: take the coefficient of the $\,x\,$ term, divide it by $\,2\,,$ and then square the result. Then:

$$ \begin{align} &\cssId{s53}{\overset{\text{start with this}}{\overbrace{x^2 + bx}}}\cr\cr &\qquad \cssId{s54}{+ \overset{\text{and add this number}}{\overbrace{ {\left(\frac{b}{2}\right)}^2}}}\cr\cr &\qquad \cssId{s55}{= \overset{\text{to get a perfect square}}{\overbrace{ {\left(x + \frac{b}{2}\right)}^2}}} \end{align} $$

Example: Identifying a Circle, Putting it in Standard Form, and Graphing

Question: Identify the graph of $\,3x^2 - 5x - 7 = 1 - 3y^2\,.$ If possible, graph the equation.

Solution: There are both $\,x^2\,$ and $\,y^2\,$ term types, and they have the same coefficient when they are on the same side of the equation.

The other terms in this equation are $\,x\,$ and constant terms, which are allowable term types for a circle.

Therefore, this is the equation of a circle. Put it in standard form as follows:

$3x^2 - 5x - 7 = 1 - 3y^2$
Original Equation
$3x^2 - 5x + 3y^2 = 8$
Put all variable terms on the left, and constant terms on the right.
$\displaystyle x^2 - \frac{5}{3}x + y^2 = \frac{8}{3}$
Divide both sides by $\,3\,.$ The coefficient of the squared term must be $\,1\,$ to use the technique of completing the square.
$\displaystyle x^2 - \frac{5}{3}x + (-\frac{5}{3\cdot2})^2 + y^2 = \frac{8}{3} + \frac{25}{36}$

There is an $\,x\,$ term, so we need to complete the square to get an expression of the form $\,(x-h)^2\,.$

On both sides, add

$$\cssId{s77}{\bigl(\frac{-5/3}{2}\bigr)^2} \cssId{s78}{= \bigl(-\frac{5}{3\cdot 2}\bigr)^2} \cssId{s79}{= \frac{25}{36}}\,,$$

which is the appropriate number to complete the square.

$\displaystyle (x - \frac{5}{6})^2 + y^2 = \frac{121}{36} $
Rename the perfect square trinomial; add fractions.
$\displaystyle (x-\frac{5}{6})^2 + (y-0)^2 = {(\frac{11}{6})}^2$
Rename to make identification easier. Thus, this is the circle with center $\,(\frac{5}{6},0)\,$ and radius $\,\frac{11}{6}\,.$

Once you know the center and radius of a circle, there are always four points that are easy to plot. Start at the center, and move up/down/left/right by the amount of the radius.

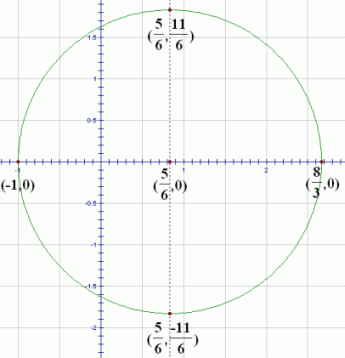
four easy points when graphing a circle

Another way to gain confidence in your work is to check at least one of these four easy points in the original equation. Let's check the point $\,(\frac{5}{6},\frac{11}{6})\,$:

$$ \begin{gather} \cssId{s92}{3x^2 - 5x - 7 = 1 - 3y^2}\cr\cr \cssId{s93}{3\left(\frac{5}{6}\right)^2 - 5\left(\frac{5}{6}\right) - 7 \ \ \overset{\text{?}}{=}\ \ 1 - 3\left(\frac{11}{6}\right)^2}\cr\cr \cssId{s94}{-\frac{109}{12} = -\frac{109}{12}}\qquad \cssId{s95}{\text{Yes!}} \end{gather} $$

Using WolframAlpha To Help With Circles

For fun, jump up to WolframAlpha and type in:

properties of 3x^2 - 5x - 7 = 1 - 3y^2

How easy is that!?

Concept Practice