Introduction to Asymptotes

DEFINITION asymptote

An ‘asymptote’ (pronounced AS-sim-tote) is a curve (usually a line) that another curve gets arbitrarily close to as $\,x\,$ approaches $\,+\infty\,,$ $\,-\infty\,,$ or a finite number.

Rational functions usually have interesting asymptote behavior.

Asymptotes exhibited by rational functions come in different flavors, as shown below:

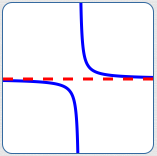horizontal asymptote

The dashed red line is horizontal.

The blue curve is getting closer and closer to this horizontal red line as $\,x\rightarrow\infty\,$ and as $\,x\rightarrow -\infty\,.$

Thus, the red line is
a horizontal asymptote.

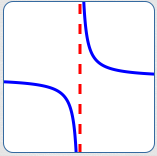vertical asymptote

The dashed red line is vertical.

The blue curve is getting closer and closer to this vertical red line as $\,x\,$ approaches a finite number (from the right, and from the left).

Thus, the red line is a vertical asymptote.

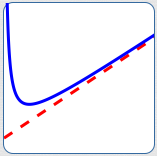slant asymptote

The dashed red line is not horizontal, and not vertical. It is ‘slanted’.

The blue curve is getting closer and closer to this ‘slanted’ red line as $\,x\rightarrow\infty\,.$

Thus, the red line is a slant asymptote.

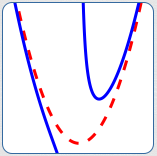asymptotes that are not lines

The dashed red curve is not a line.

The blue curve is getting closer and closer to this red curve as $\,x\rightarrow\infty\,$ and as $\,x\rightarrow -\infty\,.$

Thus, the red curve is an asymptote that is not a line.

Vertical, horizontal and slant asymptotes are studied in more detail in the next few sections.